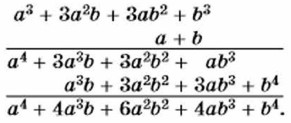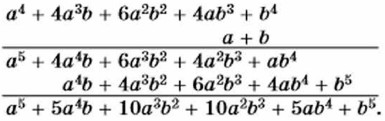Возведение двучлена в степень

Вам известны формулы квадрата суммы и квадрата разности, куба суммы и куба разности. Так как разность а - b можно рассматривать как сумму а + (-b), то в каждом случае можно говорить не о двух формулах, а об одной — квадрате двучлена и кубе двучлена:

(а + b)² = а² + 2аb + b²,

(а + b)³ = а³ + 3а²b + 3ab² + b³.

Нетрудно получить формулы для возведения двучлена в четвёртую, пятую и т. д. степень. Получить их можно последовательно одну за другой, умножая многочлен, записанный в правой части предшествующей формулы, на а + b. Например:

(а + b)⁴ = (а³ + 3а²b + 3ab² + b³)(a + b).

Умножение выполним «в столбик»:

Итак, (а + b)⁴ = а⁴ + 4а³b + 6b² + 4аb³ + b⁴.

Умножая правую часть этого равенства на а + b, получим формулу пятой степени двучлена:

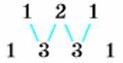
Значит,

(а + b)⁵ = а⁵ + 5а⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵.

Для того чтобы заметить закономерность в формуле n-й степени двучлена а + b при различных значениях n, выпишем их, начиная с n = 1 и заканчивая n = 5.

(a + b)¹ = а + b,

(а + b)² = а² + 2ab + b²,

(а + b)³ = а³ + 3a²b + 3ab² + b³,

(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴,

(a + b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵.

Рассматривая эти формулы, можно заметить, что в правой части каждой из них записан многочлен, содержащий n + 1 членов, где n — показатель степени двучлена.

Первый член многочлена равен аⁿ, т. е. равен произведению аⁿ и b⁰. Далее при переходе к каждому последующему члену показатель степени а уменьшается на 1, а показатель степени b увеличивается на 1, т. е. сумма показателей степеней в каждом слагаемом равна n.

Сложнее обстоит дело с коэффициентами. Чтобы выявить закономерность в их образовании, выпишем по порядку в строку коэффициенты многочленов при n = 2, а затем при n = 3:

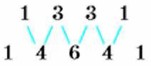
Во второй строке первый и последний коэффициенты равны 1. Нетрудно заметить, что второй коэффициент можно получить, сложив записанные над ним числа 1 и 2, третий — сложив записанные над ним числа 2 и 1.

По тому же правилу получаем строку для n = 4 из строки, записанной для n = 3:

Окончание >>>