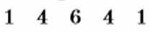|
|
|
|
|
§ 14. Преобразование целых выражений Возведение двучлена в степень (окончание)Аналогичным образом из строки
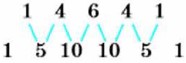
можно получить строку, в которой выписаны коэффициенты многочлена, полученного при возведении двучлена а + b в пятую степень:
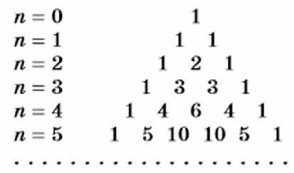
Подмеченную закономерность нетрудно обосновать, если проанализировать приведённые ранее примеры на умножение «в столбик» многочлена a3 + 3a2b + 3ab2 + b3 на двучлен а + b и многочлена а4 + 4a3b + 6a2b2 + 4ab3 + b4 на двучлен а + b. Если добавить строку для n = 0 (при а ≠ 0 или b ≠ 0), то коэффициенты всех строк можно расположить в виде треугольника:
В нём «боковые стороны» состоят из единиц, а каждое из остальных чисел равно сумме двух чисел, записанных над ним. Этот треугольник называют треугольником Паскаля но имени известного французского учёного Блеза Паскаля (1623—1662) — математика, физика, философа и литератора, описавшего такой треугольник в споём знаменитом трактате «Об арифметическом треугольнике». Продолжая запись по подмеченному правилу, мы можем получить строку коэффициентов для n = 6, 7, 8 и т. д. в формуле (а + b)n = аn + nan - 1b + ... + nabn - 1 + bn. Существует способ, позволяющий сразу найти коэффициенты многочлена для заданного n. Однако этот способ связан с понятиями, которые вам пока неизвестны. Отметим ещё одну интересную закономерность в треугольнике Паскаля. Сумма коэффициентов при n = 0, n = 1, n = 2 и т. д. равна соответственно 20, 21, 22, 23 и т. д. Вообще в равенстве (а + b)n = аn + nan - 1b + ... + nabn - 1 + bn сумма коэффициентов многочлена равна 2n. Убедиться в этом можно, подставив в это равенство а = 1 и b = 1. Упражнения 957. Напишите строки треугольника Паскаля для n = 6; n = 7. 958. Используя треугольник Паскаля, напишите формулу для шестой степени двучлена а + b. Проверьте результат, умножив на а + b многочлен, равный (а + b)5. 959. Напишите формулу: а) седьмой степени двучлена; б) восьмой степени двучлена. 960. Используя формулу четвёртой степени двучлена, преобразуйте выражение: а) (а2 + 2b)4; б) (а3 - b)4. 961. Представьте в виде многочлена выражение: а) (а2 + 3b3)3.; б) (1 - 2ху)4. 962. Представьте в виде многочлена выражение: a) (x + y)6 + (x - y)6; б) (x + y)6 - (x - y)6. 963. Выражение (1 + у)3 + (1 + у)4 + (1 + y)5 заменили тождественно равным многочленом. Найдите коэффициент члена многочлена, содержащего: а) у2; б) у3. 964. Какой остаток получится при делении числа 1476 на 145? 965. Докажите, что значение выражения: а) 834 + 65 кратно 81; б) 14110 + 88 кратно 139.
|
|
|