|
|
|
|
Главная >> Домашние работы к учебнику Макарычева. Алгебра 7 класс |
|
|
Решенния упражнений Дополнительные упражнения к параграфу 14990. а) (а2 - 7) (а + 2) - (2а - 1)(а - 14) = а3 + 2а2 - 7а - 14 - (2а2 - 28а - + 14) = а3 + (2а2 - 2а2) (-7а + 28а + а) + (-14 - 14) = а3 + 22а - 28; б) (2 - b)(1 + 2b) + (1 + b)(b3 - 3b) = 2 + 4b - b - 2b2 + b3 - 3b + b4 - 3b2 = b4 + b3 - 5b2 + 2. 991. а) (х + 4)(х2 - 4х + 16) = x3 + 64; б) (3а +5) (9а2 - 15а + 25) = 27а3 + 125. 992. а) (х + 1)(x + 2) - (х - 3)(x + 4) = 6 ⇒ х2 + 2x + х + 2 - (х2 + 4х — 3х - 12) = 6 ⇒ х2 - х2 + 3х - х = 6 - 2 - 12 ⇒ 2х = -8 ⇒ х = -4; б) (3x - 1)(2х + 7) - (х + 1)(6x - 5) = 7 ⇒ 6х2 + 21х - 2х - 7 - (6х2 - 5х + 6х - 5) = 7υ6x2 - 6х2 + 19х - х - 7 + 7 - 5 ⇒ 18х = 9 ⇒ х = 0,5; в) 24 - (3у + 1)(4у - 5) = (11 - 6у)(2у - 7) ⇒ 24 - (12у2 - 15у + 4у - 5) = 22у - 77 - 12у2 + 42у ⇒ 12у2 - 12у2 + 11у - 64у = -77 - 24 - 5 ⇒ -53у = -106 ⇒ у = 2; г) (6у + 2) (5 - у) = 47 - (2у - 3)(3у - 1) ⇒ 30у - 6у2 + 10 - 2у = 47 - (6у2 - 2у- 9у + 3) ⇒ -6у2 + 6у2 + 28у - 11у = 47 - 3 - 10 = 17у = 34 ⇒ y = 2. 993. = (2x - 5)(3 + 8x) - (1 - 4x)2 = 6x + 16х2 - 15 - 40х - (1 - 8х + 16x2) = 16х2 - 16х2 - 34x + 8х - 15 - 1 = -26х - 16 — линейная функция. А(-1; 10); -26х - 16 = 26 - 16 = 10 точка А принадлежит графику этой функции. B(0; 16); -26х - 16 = -16 ≠ 16 точка В не принадлежит графику этой функции. 994. а) (3n - 1)(n + 1) + (2n - 1)(n - 1) - (3n + 5)(n - 2) = 3n2 + 3n - n - 1 + 2n2 - 2n - n + 1 - 3n2 + 6n - 5n +10 = 2n2 +10: при n = -3,5 ⇒ 2n2 +10 = 34,5; б) (5у - 1)(2 - у) - (3у + 4)(1 - у) + (2у + 6)(у - 3) = 10у - 5у2 - 2 + у - 3у + 3у2 - 4 + 4у + 2у2 - 6у + 6у - 18 = 12у - 24: при у = 4 ⇒ 12у - 24 = 48 - 24 = 24. 995. а) (а - 3) (а2 - 8а + 5) - (а - 8) (а2 - 3а + 5) = а3 - 8а2 + 5а - 3а2 + 24а - 15 - (а3 — 3а2 + 5а - 8а2 + 24а - 40) = а3 - 11а2 + 29а - 15 - а3 + 11а2 - 29а + 40 = 25; б) (x2 - 3х + 2)(2x + 5) - (2x2 + 7х + 17)(x - 4) = 2х3 + 5х2 - 6x2 - 15x + 4x + 10 - (2x3 - 8х2 + 7х2 - 28x + 17x - 68) = 2х3 - 2х3 - x2 + х2 - 11x + 11х + 10 + 68 = 78. 996. (а2 +b2)(ab + cd) - ab • (а2 + b2 - с2 - d2) = а3b + a2cd + ab3 + b2cd - a3b - ab3 + abc2 + abd2 = (a2cd + abc2) + (b2cd + abd2) = ac • (ad + bc) + bd • (bc + ad) = (ac + bd)(ad + bc). 997. (b + c - 2 a)(c - b) + (c + a - 2 b)(a - c) - (a + b - 2c)(a - b) = ((c + b) - 2a)(c - b) + ((a + c) - 2b)(a - c) - ((a + b) - 2c) (a - b) = c2 - b2 - 2a • (c - b) + a2 - c2 - 2b • (a - c) - a2 + b2 + 2c • (a - b) = 2ab - 2ac + 2bc - 2ab + 2ac - 2bc = 0. 998. a) (a + 8)2 - 2 • (a + 8) (a - 2) + (a - 2)2 = (a + 8 - a + 2)2 = 102 = 100; 6) (y - 7)2 - 2 • (y - 7)(y - 9) + (y - 9)2 = (y - 7 - у + 9)2 = 22 = 4. 999. a) 2(a2 - 1) - (a2 + 3)(a2 - 3) - 1000. (a • (a + 2b) + b2)(a • (a - 2b) + b2)((a2 - b2)2 + 4a2b2) = (a2 + 2ab + b2)(a2 - 2ab + b2)(a4 + b4 - 2a2b2 + 4a2b2) = (a + b)2 • (a - b)2 • (a2 + b2)2 = (a2 - b2)2 • (a2 + b2)2 = (a4 - b4)2 = a8 - 2a4b4 + 68. 1001. a) (a + b)2 • (a - b) - 2ab - (b - a) - 6ab • (a - b) = (a - b)((a + b)2 + 2ab - 6ab) = (a - b)(a2 + b2 +2ab - 4ab) = (a - b)(a - b)2 = (a - b) ; 6) (a + b)(a - b)2 + 2ab • (a + b) - 2ab • (-a - b) = (a + b)(a2 - 2ab + b2 + 2ab + 2ab) = (a + b)(a + b)2 = (a + b)3. 1002. (a2 + b2)(a4 - a2b2 + b4) - (a3 - b3)(a3 + b3) = a6 + b6 - a6 + b6 = 2b6. 1003. a) (y + 5)(y2 - 5y + 25) - у • (у2 + 3) = у3 + 125 - у3 - 3у = 125 - 3у: при у - 2 ⇒ 125 - 3у = 125 + 6 = 131; б) х(х + 3)2 - (х - 1)(х2 + х + 1) = х • (х2 + 6х + 9) - х3 + 1 = х3 + 6x2 + 9х - х3 + 1 = 6х2 + 9х + 1: при х = -4 ⇒ 6х2 + 9x + 1 = 96 - 36 + 1 = 61; в) (2р - 1)(4р2 + 2р + 1) - р • (р - 1 )(р + 1) = 8р3 - 1 - р3 + р - 7р3 + р - 1: при р = 1,5 ⇒ 7р3 + р - 1 = 23,625 + 1,5 - 1 = 24,125. 1004. (р2 + cq2)(r2 + cs2) = p2r2 + p2cs2 + cq2r2 + c2q2s2 = (p2r2 + c2q2s2 + 2prcqs) + (p2cs2 + cq2r2 - 2prcqs) = (pr + cqs)2 + c • (p2s2 + q2r2 - 2prqs) = (pr + cqs)2 + c(ps - qr)2. 1005. Из (x2 + x - 1)(x - a) = x3 - ах2 + х2 - ах - x + a = x3 + x2 • (1 - a) + (-a - 1)x + а имеем, что: а) 1 - a = 0 ⇒ a = 1 — не содержит x2, при a = 1; б) -a - 1 = 0 ⇒ a = -1 — не содержит x; при a = -1. 1006. Из (x2 - 10х + 6)(2x + b) = 2x3 + 6x2 - 20x2 - 10bx + 12x + 6b = 2x3 + (b - 20)x2 + (12 - 10b)x + 6b имеем, что: а) b - 20 = 0 ⇒ b = 20 — не содержит х; при b = 20; б) 2 = 12 - 10b ⇒ 10b = 10 ⇒ b = 1 - равные коэффициенты при х3 и при х при b = 1. 1007. а) 7а3 + 7b3 = 7 • (а3 + b3) = 7 • (а + b)(а2 - аb + b2); б) 2а4 - 2b4 = 2 • (а4 - b4) = 2 • (а2 - b2)(а2 + b2) = 2 • (а - b)(а + b)(а2 + b2); в) 5а4 + 5b4 = 5 • (а4 + b4); г) 2,5а6 - 2,5b6 = 2,5 • (а6 - b6) = 2,5 • (а3 - b3)(а3 + b3) = 2,5 • (а - b)(а2 + аb + b2)(а + b)(а2 - аb + b2); д) 1,2а6 + 1,2b6 = 1,2 • (а6 + b6) = 1,2 • (а2 + b2)(а4 - а2b2 + b4); е) 3а8 - 3b8 = 3 • (а8 - b8) = 3 • (а4 - b4)(а4 + b4) = 3 • (а2 - b2)(а2 + b2)(а4 + b4) = 3 • (а - b)(а + b)(а2 + b2)(а4 + b4). <<< К началу Решенния (окончание) >>>
|
|
|



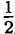 (a2 + a - 4)(2a2 + 3) = 2a4 - 4a2 + 2 - a4 + 9 -
(a2 + a - 4)(2a2 + 3) = 2a4 - 4a2 + 2 - a4 + 9 -