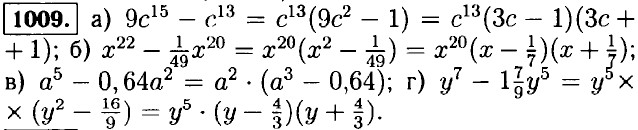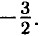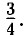Главная >> Решенния упражнений к учебнику Макарычева. Алгебра 7 класс

Домашние работы

Дополнительные упражнения к параграфу 14 (окончание)

1008. 111111 - 222 = 111 • (1001 - 2) = 111 • 999 = = 111 • 111 • 9 = (111 • 3)².

1010. а) 2x⁸ - 12x⁴ + 18 = 2 • (x⁸ - 6x⁴ + 9) = 2(x⁴ - 3)²; 6) -2a⁶ - 8a³b - 8b² = -2 • (a⁶ + 4a³b + 462) = -2(a³ + 2b)²; в) a⁴b + 6a²b³ + 9b⁵ = b • (a⁴ + 6a²b² + 9b⁴) = b(a² + 3b²)²; г) 4x + 4xy⁶ + xy¹² = x • (4 + 4y⁶ + у¹²) = x(2 + y⁶)².

1011. a) 70a - 84b + 20ab - 24b² = 10a • (7 + 2b) - 12b • (7 + 2b) = (10a - 12b)(7 + 2b) = 2 • (5a - 6b)(7 + 2b); 6) 21bc² - 6c - 3c³ + 42b = 3c² • (7b - c) + 6 • (7b - c) = (3c² + b)(7b - c) = 3 • (с² + 2)(7b - с); в) 12y - 9x² + 36 - 3x²y = 12 • (y + 3) - 3x² • (y + 3) = (12 - 3x²)(y + 3) = 3 • (4 - x²)(y + 3) = 3 • (2 - x)(2 + x)(y + 3); г) 30a³ - 18a²b - 72b + 120a = 30a • (a² + 4) - 18b • (a² + 4) = (30a - 18b)(a² + 4) = 6 • (5a - 3b)(a² + 4).

1012. а) 3а³ - 3аb² + а²b - b3 = а² • (3а + b) - b² • (3а + b) = (а² - b²)(3а + b) = (а - b)(а + b)(3а + b); б) 2х - а²у - 2а²х + у = 2x • (1 - а²) + у • (1 - а²) = (2х + у)(1 - а²) = (2х + у)(1 - а)(1 + а); в) 3р - 2с³ - 3с³р + 2 = 3р • (1 - с³) + 2 • (1 - с³) = (3р + 2)(1 - с³) = (3р + 2)(1 - с)(1 + с + с²); г) а⁴ - 24 + 8а - 3а³ = а³ • (а - 3) + 8 • (а - 3) = (а³ + 8)(а - 3) = (а + 2)(а² - 2а + 4)(а - 3).

1013. а) х³ + 3х² - 4х - 12 = 0 ⇒ х² • (х + 3) - 4 • (х + 3) = 0 ⇒ (х² - 4)(х + 3) = 0 ⇒ (х - 2)(х + 2)(х + 3) ⇒ х = ±2; и -3; б) 2m³ — m² - 18m + 9 = 0 ⇒ m² • (2m - 1) - 9 • (2m - 1) = 0 ⇒ (m² - 9)(2m - 1) = 0 ⇒ (m - 3)(m + 3)(2m - 1) = 0 ⇒ m = ±3; и 0,5; в) у³ - 6у² = 6 - у ⇒ у² • (у - 6) + (у - 6) = 0 ⇒ (у² + 1)(у - 6) = 0 ⇒ у = 6; г) 2а³ + 3а² = 2а + 3 ⇒ а² • (2а + 3) - (2а + 3) = 0 ⇒ (а² - 1)(2а + 3) = 0 ⇒ а = ±1; и

1014. а) x³ - 2x² - x + 2 = 0 ⇒ х2 • (x - 2) - (х - 2) = 0 ⇒ (х² - 1)(х - 2) = 0 ⇒ (х - 1)(х + 1)(х - 2) = 0 ⇒ х = ±1 и 2; б) y³ - y² = 16у - 16 ⇒ у² • (у - 1) - 16 • (у - 1) = 0 ⇒ (у² - 16)(у - 1) = 0 ⇒ (у - 4)(у + 4)(у - 1) = 0 ⇒ у = ±4 и 1; в) 2у³ - у² - 32у + 16 = 0 ⇒ у² • (2у - 1) - 16 • (2у - 1) = 0 ⇒ (у² - 16)(2у - 1) = 0 ⇒ (у - 4)(у + 4)(2у - 1) = 0 ⇒ у = ±4 и 0,5; г) 4х³ - 3х² - 4х - 3 ⇒ х² • (4х - 3) - (4х - 3) = 0 ⇒ (х - 1)(х + 1)(4х - 3) = 0 ⇒ х = ±1 и

1015. а) х² - у² - 1,5 • (х - у) = (х - у)(х + у) - 1,5 • (х - у) = (х - у)(х + у - 1,5); б) х² - а² + 0,5 • (х + а) - (х - а)(х + а) +0,5 • (х + а) = (х + а)(х - а + 0,5); в) 4а² - b² - 2а + b = (2а - b) (2а + b) - (2а - b) = (2а - b)(2а + b - 1); г) р² - 16с² - р - 4с = (р - 4с)(р + 4с) - (р + 4с) = (р + 4с)(р - 4с - 1); д) а² + 6а + 6b - b² - (а - b)(а + b) + 6 • (а + b) = (а + b)(а - b + 6); е) х² - 7х + 7у - у² = (х - у)(х + у) - 7 • (х - у) = (х - у)(х + у - 7).

1016. а) х² • (х + 2у) - x - 2у - (х² - 1)(х + 2у) = (х - 1)(х + 1)(х + 2у); б) х² • (2у - 5) - 8у + 20 = (х² - 4)(2у - 5) = (х - 2)(х + 2)(2у - 5); в) а³ - 5а² - 4а + 20 = а² • (а - 5) - 4 • (а - 5) = (а² - 4)(а - 5) = (а - 2)(а + 2)(а - 5); г) х³ - 4х² - 9х + 36 = х² • (х - 4) - 9 • (х - 4) = (х - 3)(х + 3)(х - 4).

1017. а) а² - b² + 2(а + b) = (а - b)(а + b) + 2(а + b)² = (а + 6)(а - b + 2а + 2b) = (а + b)(3а + b); б) b² - с² - 10(b - с)² = (b - с)(b + с) - 10(b - с)² = (b - с)(b + с - 10b + 10с) = (b - с) (11с - 9b); в) 2(х - у)² + 3х² - 3у² = 2 • (х - у) (х - у) + 3 • (х - у) (х + у) = (х - у)(2х - 2у + 3х + 3у) = (х - у)(5х + у); г) 5а² - 5 - 4(а + 1)² = 5 • (а - 1)(а + 1) - 4(а + 1)² = (а + 1)(5а - 5 - 4а - 4) = (а + 1)(а - 9).

1018. а) а² + b² - 2аb - 25 = (а - b)² - 25 = (а - b - 5)(а — b + 5); б) 36 - b² - с² + 2bс = 36 - (b - с)² = (6 - b + с)(6 + b - с); в) 49 - 2ах - а² - х² = 49 - (а + х)² = (7 - а - х)(7 + а + х); г) b² - а² - 12а - 3b = b² - (а + b)² = (b - а - 6)(b + а + 6); д) 81а² + 6bс - 9b² - с² - 81а² - (3b - с)² = (9а - 3b + с)(9а + 3b - с); e) b²c² - 4bc - b² - с² + 1 = (bc - 1)² - (b + c)² = (bc - 1 - b - c)(bc - 1 + b + c).

1019. a) x³ + y³ + 2xy • (x + y) = (x + y)(x² - xy + y²) + 2xy • (x + y) = (x + y)(x² - xy + y² + 2xy) = (x + y)(x² + xy + y²); 6) x³ - y³ - 5x • (x² + xy + y²) = (x - y)(x² + xy + y²) - 5x • (x² + xy + y²) = (x - у - 5x) (x² + xy + y²) = (-4x - y)(x² + xy + y²); в) 2b³ + a • (a² - 3b²) = 2b³ + a³ - 3ab² = a3 - b³ + 3b³ - 3 ab² = (a - b)(a² + ab + b²) - 3b² • (a - b) = (a - b)(a² + ab - 2b²); г) p³ - 2p² + 2p - 1 = (p³ - 1) - 2p • (p- 1) = (p - 1)(p² + p + 1) - 2p • (p - 1) = (p - 1)(p² - p + 1); д) 8b³ + 6b² + 3b + 1 = (8b³ + 1) + 3b • (2b + 1) = (2b + 1)(4b - 2b + 1) + 3b • (2b + 1) = (2b + 1)(4b + b + 1); е) a³ - 4a² + 20a - 125 = (a³ - 125) - 4a • (a - 5) = (a - 5) (a² + 5a + 25) - 4a • (a - 5) = (a - 5)(a² + a + 25).

1020. а) x³ + у³ + 2x² - 2xy + 2у² = (x + y)(x² - xy + y²) + 2 • (x² - xy + у²) = (x + у + 2)(x² - xy + y²); 6) a³ - b³ + 3a² + 3ab + 3b² = (a - b)(a² + ab + b²) + 3 • (a² + ab + b²) = (a - b + 3)(a² + ab + b²); в) a⁴ + ab³ - a³b - b⁴ = a • (a³ + b³) — b • (a³ + b³) = (a - b)(a³ + b³) = (a - b)(a + b)(a² - ab + b²); г) x⁴ + x³y - xy³ - y⁴ = x • (x³ - у³) + у • (x³ - y³) = (x + y)(x³ - y³) = (x + y)(x - y)(x² + xy + y²).

1021. a) x² - 2xy + y² + a² = (x - y)² + a² ≥ 0; 6) 4x² + a² - 4x + 1 = (2x — 1)² + a² ≥ 0; в) 9b² - 6b + 4c² + 1 = (3b - 1)² + 4c² ≥ 0; г) a² + 2ab + 2b² + 2b + 1 = (a + b)² + (b + 1)² ≥ 0; д) x² - 4xy + y² + x²y² + 1 = (x - y)² + (xy - 1)² ≥ 0; e) x² + y² + 2x + 6y + 10 = (x + 1)² + (у + 3)² ≥ 0.

1022. a) a² + 16a + 64 = (a + 8)² ≥ 0; — нет, данное выражение не может принимать отрицательные значения, так как квадрат любого числа не отрицателен; б) -b² - 25 + 10b = -(b - 5)² ≤ 0; нет, данное выражение не может принимать положительные значения; в) -x² + 6x - 9 = -(x - 3)² ≤ 0; — данное выражение может принимать не отрицательные значения, например при x = 3; -(x - 3)² = 0; г) (у + 10)² - 0,1; — данное выражение может принимать отрицательные значения, например при у = -10; (у + 10)² - 0,1 = -0,1; д) 0,001 - (а + 100)²; — данное выражение может принимать положительные значения, например при а = -100; 0,001 - (а + 100)² = 0,001.

1023. а) (2n + 3)(3n - 7) ² (n + 1)(n - 1) = 6n² - 14n + 9n - 21 - n² + 1 - 5n² - 5n - 20 = 5 • (n² - n - 4) — кратно 5; б) (7n + 8)(n - 1) + (3n - 2)(n + 2) = 7n² - 7n + 8n - 8 + 3n² + 6n - 2n - 4 = 10n² + 5n - 12 = 5 • (2n² + n - 3) + 3 — не кратно 5.

1024. (10n + 5)² = 100n² + 100n + 25 = 100n • (n + 1) + 25; 25² = 100 • 2 • (2 + 1)+ 25 = 625; 45² = 100 • 4 • (4+ 1) + 25 - 2025; 75² = 100 • 7 • (7 + 1) + 25 = 5625; 115² = 100 • 11 • (11 + 1) + 25 = 13225.

<<< К началу