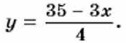Линейное уравнение с двумя переменным

Пусть известно, что одно из двух чисел на 5 больше другого. Если первое число обозначить буквой х, а второе — буквой у, то соотношение между ними можно записать в виде равенства х - у = 5, содержащего две переменные. Такие равенства называют уровнениями с двумя переменными или уравнениями с двумя неизвестными.

Приведём другие примеры уравнений с двумя переменными: 5x + 2у = 10, -7х + у = 5, х² + у² = 20, ху = 12. Из этих уравнений первые два имеют вид ах + by = с, где а, b и с — числа. Такие уравнения называют линейными уравнениями с двумя переменными.

Определение. Линейным уравнением с двумя переменными называется уравнение вида ах + by = с, где х и у — переменные, а, b и с — некоторые числа.

Уравнение х - у = 5 при х = 8, у = 3 обращается в верное равенство 8 - 3 = 5. Говорят, что пара значений переменных х = 8, у = 3 является решением этого уравнения.

Определение. Решением уравнения с двумя переменными называется пара значений переменных, обращающая ото уравнение в верное равенство.

Нетрудно проверить, что решениями уравнения х - у = 5 являются также пары: х - 105, у = 100; х = 4, у = -1; х = 3,5, у = -1,5. Пары значений переменных записывают иногда короче. Например, перечисленные пары можно записать так: (105; 100), (4; -1), (3,5; -1,5). При такой записи необходимо знать, значение какой из переменных стоит на первом месте, а какой — на втором. В записи решений уравнения с переменными хну условимся на первом месте записывать значения х, а на втором — значения у.

Уравнения с двумя переменными, имеющие одни и те же решения, называют равносильными. Уравнения с двумя переменными, не имеющие решений, также считают равносильными.

Уравнения с двумя переменными обладают такими же свойствами, как и уравнения с одной переменной:

если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному;
если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

Рассмотрим уравнение

5х + 2y =12. (1)

Воспользовавшись свойствами уравнений, выразим из этого уравнения одну переменную через другую, например у через х. Для этого перенесём слагаемое 5х в правую часть уравнения, изменив его знак:

2у = -5х + 12.

Разделим обе части этого уравнения на 2:

у = -2,5х + 6. (2)

Уравнение (2) равносильно уравнению (1). Пользуясь формулой у = -2,5x + 6, можно найти сколько угодно решений уравнения (1). Для этого достаточно взять произвольное x и вычислить соответствующее ему значение у. Например:

если x = 2, то у = -2,5 • 2 + 6=1;

если х = 0,4, то у = -2,5 • 0,4 + 6 = 5.

Пары чисел (2; 1), (0,4; 5) — решения уравнения (1). Уравнение (1) имеет бесконечно много решений.

Иногда при решении задачи требуется найти все пары целых чисел или все пары натуральных чисел, удовлетворяющие уравнению с двумя переменными. В таких случаях говорят, что надо «решить уравнение в целых числах» или «решить уравнение в натуральных числах».

Проблема решения уравнений в натуральных числах подробно рассматривалась в работах известного греческого математика Диофанта (III в.). В его трактате «Арифметика» приводятся остроумные способы решения в натуральных числах самых разнообразных уравнений. В связи с этим уравнения с несколькими переменными, для которых требуется найти решения в натуральных или целых числах, называют диофантовыми уравнениями.

Рассмотрим задачу, в которой надо найти натуральные решения уравнения с двумя переменными.

Задача. Группу из 35 туристов решили расселить на теплоходе в трёхместные и четырёхместные каюты так, чтобы в каютах не оставалось свободных мест. Сколько трёхместных и сколько четырёхместных кают надо заказать?

Допустим, что надо заказать * трёхместных и у четырёхместных кают. Тогда

3x + 4у = 35.

Требуется найти все пары натуральных значений переменных * и у, удовлетворяющие этому уравнению.

Из уравнения 3х + 4у = 35 находим, что

Подставляя в это равенство вместо * последовательно числа 1, 2, 3 и т. д., найдём, при каких натуральных значениях * соответствующие значения у являются натуральными числами: если х = 1, то у = 8; если x = 5, то у = 5; если x = 9, то у = 2. Других пар натуральных чисел, удовлетворяющих уравнению 3x + 4у = 35, нет, так как при других натуральных значениях x соответствующее значение у является либо дробным положительным числом, либо отрицательным числом.

Значит, надо заказать соответственно трёхместных и четырёхместных кают либо 1 и 8, либо 5 и 5, либо 9 и 2.

Окончание >>>