|
|
|
|
|
Дополнительные упражнения к главе 5 К параграфу 14990. Представьте в виде многочлена: а) (а2 - 7)(а + 2) - (2а - 1)(а - 14); б) (2 - b)(1 + 2b) + (1 + b)(b3 - 3b). 991. Представьте в виде многочлена: а) (х + 4)(х2 - 4х + 16); б) (3а + 5)(9а2 - 15а + 25). 992. Решите уравнение: а) (х + 1)(х + 2) - (х - 3)(х + 4) = 6; б) (3х - 1)(2х + 7) - (х + 1)(6х - 5) = 7; в) 24 - (3у + 1)(4у - 5) = (11 - 6у)(2у - 7); г) (6у + 2)(5 - у) = 47 - (2у - 3)(3y - 1). 993. Докажите, что функция» заданная формулой y = (2х - 5)(3 + 8х) - (1 - 4x)2, линейная. Принадлежит ли графику этой функции точка А(-1; 10)? точка В(0; 16)? 994. Найдите значение выражения: а) (3n - 1)(n + 1) + (2n - 1)(n - 1) - (3n + 5)(n - 2) при n = -3,5; б) (5у - 1)(2 - у) - (3у + 4)(1 - у) + (2у + 6)(у - 3) при у = 4. 995. Докажите, что значение выражения не зависит от значения переменной: а) (а - 3)(а2 - 8а + 5) - (а - 8)(а2 - 3а + 5); б) (х2 - 3х + 2)(2х + 5) - (2х2 + 7х + 17)(х - 4). 996. Докажите тождество (а2 + b2)(аb + cd) - ab (а2 + b2 - с2 - d2) = (ас + bd)(ad + bс). 997. Докажите» что значение выражения (b + с - 2а)(с - b) + (с + а - 2b)(а - с) - (а + b - 2с)(а - b) при любых значениях а, b и с равно 0. 998. Упростите выражение: а) (а + 8)2 - 2(а + 8)(а - 2) + (а - 2)2; б) (у - 7)2 - 2(у - 7)(y - 9) + (у - 9)2. 999. Упростите: а) 2(а2 - 1)2 - (а2 + 3)(а2 - 3) - б) 4(m3 - 3)2 - (m2 - 6)(m2 + 6) - 9(8 - m + m2)( 1 - m). 1000. Представьте в виде многочлена (а(а + 2b) + b2)(а(а - 2b) + b2)((а2 - b2)2 + 4а2b2). 1001. Докажите тождество: а) (а + b)2(а - b) - 2аb(b - а) - 6аb(а - b) = (а - b)3; б) (а + b) (а - b)2 + 2аb(а + b) - 2аb(-а - b) = (а + b)3. 1002. Докажите тождество (а2 + b2) (а4 - а2b2 + b4) - (а3 - b3)(а3 + b3) = 2b6. 1003. Найдите значение выражения: а) (y + 5) (у2 - 5у + 25) - y(y2 + 3) при y = -2; б) х(х + 3)2 - (x - 1)(x2 + х + 1) при х = -4; в) (2р - 1)(4р2 + 2р + 1) - р(р - 1)(р+ 1) при р = 1,5. 1004. В книге Леонарда Эйлера (XVIII в.) используется тождество (р2 + сq2) (r2 + cs2) = (pr + сqs)2 + c(ps - qr)2. Докажите его. 1005. При каком значении а многочлен стандартного вида, тождест венно равный произведению (х2 + х - 1)(х - а), не содержит: а) х2; б) х? 1006. При каком значении 6 многочлен стандартного вида, тождест венно равный произведению (х2 - 10х + 6)(2х + 6): а) не содержит х2; б) имеет равные коэффициенты при х3 и при х?
|
|
|



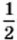 (а2 + а - 4)(2а2 + 3);
(а2 + а - 4)(2а2 + 3);