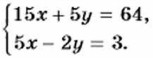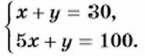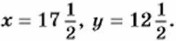Решение задач с помощью систем уравнений

При решении задач с помощью систем уравнений поступают следующим образом:

1) обозначают некоторые неизвестные числа буквами и, используя условие задачи, составляют систему уравнений;
2) решают эту систему;
3) истолковывают результат в соответствии с условием задачи.

Задача 1. Масса 15 кирпичей и 5 шлакоблоков равна 64 кг. Какова масса одного кирпича и одного шлакоблока, если 5 кирпичей тяжелее 2 шлакоблоков на 3 кг?

Пусть масса кирпича х кг, а шлакоблока у кг. Тогда масса 15 кирпичей и 5 шлакоблоков будет 15х + 5у кг. По условию задачи она равна 64 кг, поэтому 15х + 5у = 64.

Известно, что 5 кирпичей тяжелее 2 шлакоблоков на 3 кг. Значит,

5х - 2у = 3.

Чтобы ответить на вопрос задачи, надо найти такие значения х и у у которые удовлетворяют как первому, так и второму уравнению, т. е. удовлетворяют системе

Решив эту систему, получим, что х = 2,6, у = 5.

Ответ. Масса кирпича 2,6 кг, а шлакоблока 5 кг.

Задача 2. Молено ли разменять сторублёвую купюру пятирублёвыми и однорублёвыми монетами так, чтобы всех монет было 30?

Допустим, что следует взять х пятирублёвых и у однорублёвых монет. По условию х + у = 30. Так как с помощью этих монет нужно разменять 100 р., то должно выполняться равенство 5х + у = 100. Получили систему уравнений

Решив её, найдём, что

По смыслу задачи х и у должны быть натуральными числами, а мы получили дробные числа.

Ответ. Разменять сторублёвую купюру указанным способом невозможно.

Упражнения

1099. В фермерском хозяйстве под гречиху и просо отведено 19 га, причём гречиха занимает на 5 га больше, чем просо. Сколько гектаров отведено под каждую из этих культур?

1100. Техническое перевооружение цеха позволило выпустить в феврале на 165 изделий больше, чем в январе. Сколько изделий было выпущено в январе и сколько в феврале, если известно, что за эти месяцы цех выпустил 1315 изделий?

1101. В мастерской «Автосервис» отремонтировали 22 легковых и грузовых автомобиля. Среди них легковых было на 8 меньше, чем грузовых. Сколько грузовых автомобилей отремонтировали в мастерской?

1102. На теннисном корте для игры пар теннисистов выделяется площадка прямоугольной формы. Найдите длину и ширину площадки, если известно, что длина больше ширины на 12,8 м, а периметр прямоугольника равен 69,48 м.

1103. Основание равнобедренного треугольника на 7 см больше его боковой стороны. Найдите боковую сторону треугольника, если его периметр равен 43 см.

1104. Старинная задача. Ослица и мул шли вместе, нагруженные равными но весу мешками. Ослица жаловалась на тяжесть ноши. «Что ты жалуешься, — сказал мул, — если ты дашь мне твой мешок, моя ноша станет вдвое больше твоей, а если я тебе дам один мешок, то наши грузы сравняются». Сколько мешков нёс каждый?

1105. Старинная задача. Если А получит от B 100 рупий, то станет вдвое его богаче, а если A даст B 10 рупий, то Я станет вшестеро богаче. Сколько денег у каждого?

1106. Сколько лет брату и сколько лет сестре, если 2 года назад брат был старте сестры в 2 раза, а 8 лет назад — в 5 раз?

1107. Два автомата изготавливают детали. Число деталей, изготовленных первым автоматом за 3 ч и вторым за 2 ч, составляет 720 штук. Четвёртая часть деталей, изготовленных обоими автоматами за 2 ч, составила 150 штук. Сколько деталей изготовлял каждый автомат за час?

1108. За 4 ч езды на автомашине и 7 ч езды на поезде туристы проехали 640 км. Какова скорость поезда, если она на 5 км/ч больше скорости автомашины?

1109. Теплоход проходит за 3 ч по течению и 2 ч против течения 240 км. Этот же теплоход за 3 ч против течения проходит на 35 км больше, чем за 2 ч по течению. Найдите скорость теплохода против течения и его скорость но течению.

1110. Из пунктов A и B, расстояние между которыми равно 280 км, выходят одновременно два автомобиля. Если автомобили будут двигаться навстречу друг другу, то встреча произойдёт через 2 ч. Если же они будут двигаться в одном направлении, то автомобиль, вышедший из А, догонит автомобиль, вышедший из B, через 14 ч. Какова скорость каждого автомобиля?

Окончание >>>