|
|
|
|
Главная >> Домашние работы к учебнику Макарычева. Алгебра 7 класс |
|
|
Решенния задач
Задачи повышенной трудности1184. (а = 1)x = 12; а - 1 ≠ 0; а ≠ 1; 1185. а) |x - 3| = 7: при x ≥ 3; |x - 3| = x - 3 ⇒ x - 3 = 7; x = 10; при x < 3; |x - 3| = -x + 3 ⇒ -x + 3 = 7; x = -4. Ответ: x = -4; 10. б) |x + 2| = 9: при x ≥ -2; |x + 2| = x + 2 ⇒ x + 2 = 9; x = 7; при x < -2; |x + 2| = -x - 2 ⇒ -x - 2 = 9; -x = 11; x = -11. Ответ: x = -11; 7. в) (4 - x| = 1,5: при x ≥ 4; |4 - x| = x - 4 ⇒ x - 4 = 1,5; x = 5,5; при x < 4; |4 - x| = 4 - x ⇒ 4 - x = 1,5; x = 2,5; Ответ: x = 2,5; 5,5. г) |6 - x| = 7,3: при x ≥ 6; |6 - x| = x - б ⇒ x - 6 = 7,3; x = 13,3; при x < 6; |6 - x| = 6 - x ⇒ 6 - x = 7,3; x = -1,3. Ответ: x = -1,3; 13,3. 1186. Шестизначное число, в котором первая цифра совпадает с четвёртой, вторая — с пятой и третья — с шестой можно представить как 1187. Пусть в первой бочке ж воды, во второй бочке тогда тоже ж. После того как количество воды в первой бочке уменьшили на 10%, в ней стало 0,9ж воды. Затем увеличили на 10%, 0,9x + 0,9x • 0,1 = 0,99x. Во второй бочке объём воды увеличили на 10%, в ней стало 1,1x. Затем уменьшили на 10%, 1,1x - 1,1x • 0,1 = 0,99ж. Ответ: В бочках стало одинаковое количество воды. 1188. В 11 кг свежих грибов содержится 11 • 0,9 = 9,9 кг воды. Вес грибов без воды составляет 11 - 9,9 = 1,1 кг. В сухих грибах 12% воды, 100% -12% = 88%. Значит масса сухих грибов равна
1190. 13 + 23 ... +993 сгруппируем члены суммы таким образом, (13 + 993) + (23 + 983) + (33 + 973) + (43 + 963) + ... без пары останется только 503, (1 + 99)(1 - 99 + 992) + (2 + 98) (22 - 98 • 2 + 982) + ... + (49 + 51)(492 - 49 • 51 + 512) + 503 = 100 • (1 - 99 + 992 + 22 - 98 • 2 + 982 + ... + 492 - 49 • 51 + 512) + 1000 • 53 = 100 • (1 - 99 + 992 + 22 - 98 • 2 + 982 + ... + 492 - 49 • 51 + 512 + 10 • 53) - делится на 100.
1193. Пусть количество десятков искомого числа равняется а, а единиц b. Тогда, 10а + b = 4 • (а + b); 10а + 6 = 4а + 46; 6а = 3b2а = 6. Переменная а принимает значения от 1 до 9, а b от 0 до 9: при а = 1, b = 2; при а = 2, b = 4; при а = 3, b = 6; при а = 4, b = 8; Ответ: 12, 24, 36, 48.
1194. 1195. Пусть х простое число, у частное, остаток z. х - z = 30b. Проведём доказательство от противного. Предположим что остаток от деления составное число, 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28 все возможные составные остатки. Число z не может быть чётным, так как х было бы чётным, противоречит условию. Тогда остаются остатки 9, 15, 21, 25, 27. Все эти числа кроме 25 можно представить в виде 3n, где n ∈ N. Пусть z = 3n. х - 3n = 30y. х = 3 • (10у + 1), но х простое — противоречие. Пусть z = 25х - 25 = 30у, х = 5 • (6у + 5), х — кратно 5 — противоречие. Значит z может быть простым числом или единицей.
1196. 10а + 1000 + 1 = 23а ⇒ 10а + 1001 = 23а ⇒ 13а = 1001 ⇒ а = 77. Ответ: 77.
1197. 1. Зачеркнули первую цифру тогда 10а + b = 31b. 3b = а: при b = 1, а = 3; при b = 2, а = 6; при b = 3, а = 9.
2. Зачеркнули вторую цифру 10а + b = 31а; b = 21а — не имеет решения, так как переменная а принимает значения от 1 до 9, а 6 от 0 до 9. Ответ: в числах 31, 62, 93 зачеркнули первую цифру.
1198. Пусть первоначальное число 1199. а) (х - 2) (у + 3) = 0 ⇒ х = 2; у = -3;
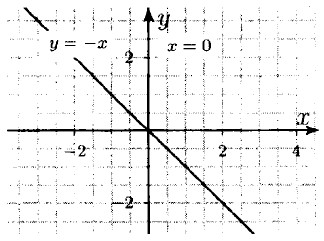
б) х2 + ху ⇒ х • (х 4- у) = ⇒ х = 0; у = -х.
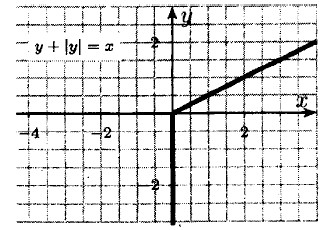
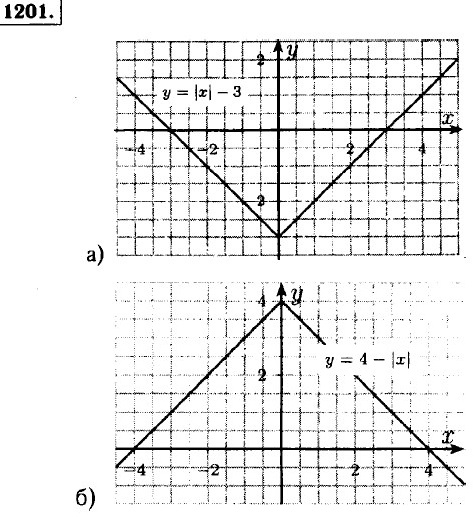
1200. а) у + |у| = х: при у ≥ 0 ⇒ |у| = у ⇒ у - 0,5x; при у < 0 ⇒ |у| = -у ⇒ х = 0;
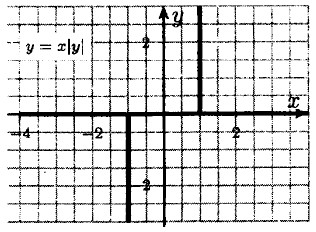
б) у = х|у|: при у > 0 ⇒ |у| = у ⇒ х = 1; при у < 0 ⇒ |у| = -у ⇒ а; = -1; при у = 0 ⇒ x — любое.
1202. 1. Если после умножения на 2 искомое число станет квадратам, значит в разложении на простые множители этого числоколичество 2 не чётно, а всех остальных равных членов произведения чётное кол- личество. 2. После умножения на 3 станет кубом, значит если к числу троек в разложении на простые множители в искомом числе прибавить ещё одно, то их количество должно делится на 3. А все остальные равные члены произведения являются кубом какого-то числа. Очевидно, что искомое число в разложении на простые множители должно содержать 2 и 3. Из 1 и 2 следует, что минимальное количество двоек 3, а троек 2. Искомое число 2 • 2 • 2 • 3 • 3 = 72.
1203. 967 оканчивается на 6. 225 оканчивается на 2, т. к. 25 = 32. 486 оканчивается на 4, т. к. 86 = 23 • 6 = 218 оканчивается на 4, значит 967 - 225 - 486 оканчивается на 6 - 2 - 4 = 0 следовательно кратно 10.
2004.
<<< К началу Решенния (окончание) >>>
|
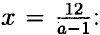а = 2 ⇒ x = 12; а = 3 ⇒ x = 6; а = 4 ⇒ x = 4; а = 5 ⇒ x = 3; а = 7 ⇒ x = 2; а = 13 ⇒ x = 1. Ответ: а = 2; 3; 4; 5; 7; 13.
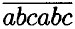где переменные b, с принимают значения от 0 до 9, а переменная а от 1 до 9: 
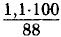= 1,25 кг. Ответ: 1,25 кг.
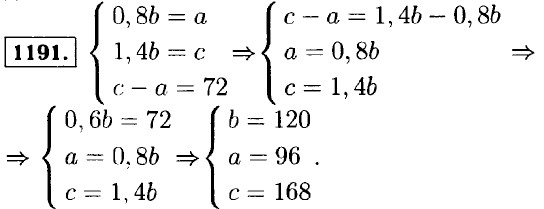
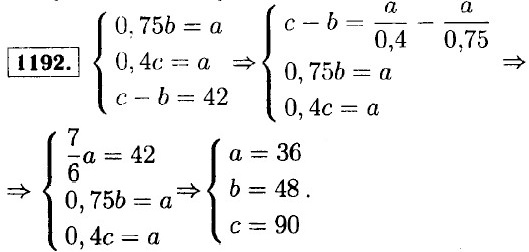
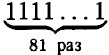= 111111111 • 1072 + 111111111 • 1063 + ... s + 111111111 = 111111111 • (1072 + 1063 + • • • 1). Число 111111111 делится на 9 так как сумма его цифр кратна 9, (1072 + 1063 + • • • + 1) сумма цифр равна 9 значит так же делится на 9. Значит 
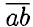= 10a + b; где переменная a принимает значения от 1 до 9, а b от 0 до 9.
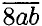= 800 + 10а + b; где переменные а и b принимают значения от 0 до 9. Тогда, 800 + 10а + b + 18 = 100а + 10b + 8 ⇒ 810 = 90а + 9 ⇒ 90 = 10а + b ⇒ а = 9 и b = 0. Ответ: 890.
|
|