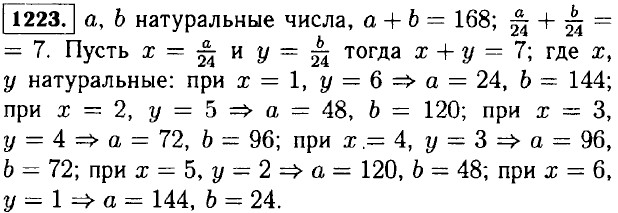|
|
|
|
Главная >> Решенния задач к учебнику Макарычева. Алгебра 7 класс |
|
|
Домашние работы Задачи повышенной трудности (окончание)1205. Умножим обе части на (1011 + 1)(1012 + 1); (1010 + 1)(1012 + 1)?(1011 + 1)(1011 + 1); 1022 + 1012 + 1010 +1?1022 + 2 • 1011 + 1; вычтем 1022 + 1; 1010(102 + 1)?1010(2 • 10); разделим обе части на 1010; 101 > 20. Значит 1206. 2х2 + 2у2 = (х2 + 2ху + у2) + (х2 - 2ху + у2) = = (х + у)2 + (х - у)2; 1207. 15х2 - 18ху + 15у2 = (9х2 - 18ху + 9у2) + 6х2 + 6у2 = (3x - 3у)2 + 6у2 + 6х2 > 0, т. к. 6у2 > 0; 6x2 > 0; (3x — 3у)2 ≥ 0. 1208. а) х8 + х4 - 2 = (х8 - 1) + (х4 - 1) = (х4 - 1)(х4 + 1) + (х4 - 1) = (х4 - 1)(х4 + 2) = (х - 1)(х + 1)(х2 + 1)(х4 + 2); б) а5 - а2 - а - 1 = а • (а4 - 1) - (а2 +1) = а • (а2 - 1)(а2 + 1) - (а2 + 1) = (а2 + 1)(а3 - а - 1); в) n4 + 4 - n4 + 4n2 + 4 - 4n2 = (n2 + 2)2 - (2n)2 = (n2 -2n + 2)(n2 + 2n + 2); г) n4 + n2 + 1 = (n4 + 2n2 + 1) - n2 = (n2 + 1)2 - n2 - (n2 - n + 1)(n2 + n + 1). 1209. Имеем р2 - 1 = (р + 1 )(р - 1), т. к. р простое число больше 3, значит р нечётное, и следовательно р + 1 и р - 1 последовательные чётные числа, причём одно из них кратно 4. Значит (р + 1 )(р - 1) делится на 2 • 4 = 8; Из чисел 3 последовательных чисел обязательно одно делится на 3 и так как р простое и не кратно 3, из чисел р + 1 и р - 1 обязательно одно делится на 3. Значит (р + 1)(р - 1) кратно 3 • 8 = 24. 1210. Имеем (n + 1)3 - n3 = n3 + 3n2 + 3n + 1 - n3 = 3 • (n2 + n) + 1; n2 + n — при чётном п кратно 2, при не чётном n также кратно 2 так как сумма двух нечётных чисел равна чётному числу. Значит 3 • (n2 + n) — делится на 6, a (n + 1)3 - n3 при делении на 6 даёт остаток 1. 1211. Имеем а - 2, а - 1, а, а + 1, а + 2 — пять последовательных натуральных чисел (а ≥ 3); (а - 2) + (а — 1)2 + а2 + (а + 1)2 + (а + 2)2 = а2 - 4а + 4 + а2 - 2а + 1 + а2 + а2 + 2а + 1 = а2 + 4а + 4 = 5а2 + 10; 1. Пусть а чётное, тогда а2 = 4n, где n — натуральное число. 5а2 + 10 = 20n + 10 = 10 • (2n + 1) = 5 • (4n + 2) = 2 • (10n + 5) — не может быть квадратом натурального числа, так как 10n + 5 всегда не чётное, значит при разложении числа 2 • (10n + 5); 2 встречается всего один раз. 2. Пусть а — не чётное, тогда а2 = 2n + 1, где n — некоторое натуральное число. 5а2 + 10 = 10n + 15 = 5 • (2n + 3). Мы представили 5а2 + 10 в виде произведения двух натуральных чисел. Значит 2n + 3 = 5, n = 1, 5а2 + 10 = 25; 5а2 = 15, а2 = 3. Натурального числа, квадрат которого равен 3 не существует, следовательно, если а — нечётное, то 5а2 + 10 нельзя представить в виде квадрата некоторого натурального числа. Рассмотрены все случаи. Утверждение доказано. 1212. Если число не кратно 3 то оно даёт в остатке при делении на три 1 или 2. 1. Остаток равен 1. (3n + 1)2 - 1 = 9n2 + 6n + 1 - 1 = 9n2 + 6n = 3 • (3n2 + 2n). 2. Остаток равен 2. (3n + 2)2 - 1 = 9n2 + 12n + 4 - 1 = 3 • (3n2 +4n + 1). 1213. (2 + 1)(22 + 1)(24 + 1)(28 + 1)(216 + 1)(232 + 1) = (2 - 1)(2 + 1)(22 + 1)(24 + 1)(28 + 1)(216 + 1)(232 + 1) = (22 - 1)(22 + 1)(24 + 1)(216 + 1)(232 + 1) = (24 - 1)(24 + 1)(216 + 1)(232 + 1) = (216 - 1)(216 + 1)(232 + 1) = (232 - 1)(232 + 1) - 264 - 1. 1214. Дано х2 - у2 = 30. Так как х2 = (-х)2 будем рассматривать только положительные числа и ноль. То есть х ≥ 0, у ≥ 0. 1. Пусть х = n, у = 2k. х2 - у2 = 4 • (n2 - k2) = 30; 2 • (n2 - k2) = 15, но х и у целые числа. Значит данное выражение не имеет решений. 2. Пусть х = 2n + 1, у = 2k + 1; х2 - у2 = (2n + 1)2 - (2к + 1)2 = 4 • (n2 + n - k2 - k) = 30; 2 • (n2 + n - k2 - k) = 15. Очевидно, что при целых п и к не имеет решений. 3. При х чётном, а у нечётном или наоборот, х2 - у2 будет нечётное число (в результате вычитания из чётного числа нечётное получится чётное) но должно быть чётным. Противоречие. Значит х2 - у2 = 30 не имеет целых решений.
1216. Дано: у = 1217. Дано: p2 - 2q2 = 1 ⇒ 2q2 = p2 - 1 ⇒ 2q2 = (p - 1)(p + 1). 1. Пусть p чётное. Единственное чётное простое число это 2. 2q2 = 3. Не может быть такого при простом q. 2. Пусть р не чётное. Тогда р = 2n + 1 где n какое то натуральное число, тогда (р - 1 )(р + 1) = (2n + 1 - 1)(2n + 1 + 1) = 4n • (n + 1), значит q2 = 2n • (n + 1), а значит q кратно 2. Единственное простое число которое делится на 2 это 2. q = 2. 8 = р2 - 1; р2 = 9; p = 3. Ответ: q = 2, р = 3. 1218. 5х3 - 32х2 + 75х - 71; а(х - 2)3 + 6(х - 2)2 + с • (х - 2)+d = а • (х3 - 3х2 • 2 + 3х • 4 - 8) + 6 • (х2 - 4х + 4) + сх -; -2с + d = ах3 - 6ах2 + 12ах - 8а + bх2 - 4bх + 4b + сх - 2с + d = ах3 + (-6а + b)х2 + (12а - 4b + с)х + (-8а + 4b - 2с + d). Значит 5х3 = ах3; а = 5; (-6а + b)х2 = -32х2; -30 + b = -32; b = -2; (12а - 4b + с)х = 75х; 60 + 8 + с = 75; с = 7; -8а + 4b -2c + d= -71; -40 - 8 - 14 + d = 71; d = -9. Ответ: а = 5, b = -2, с = 7, d = -9. 1222. Если трёхзначное число равно квадрату двухзначного и кубу однозначного, значит это 6 степень какого-то однозначного числа, подходит только 3, значит искомое число 36 = 93 = 272 = 729. Ответ: 729.
1224. Выпишем все простые числа меньше 26: 2, 3, 5, 7, 11, 13, 17, 19, 23. Из х + у = 26 имеем, что: х = 3, у = 23; х = 7, у = 19; х = 13; у = 13; х = 19, y = 7; х = 23, у = 3.
|
|
|



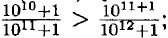

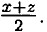 х4 + 2x3z — 2xz3 - z4 - 4х2у2 + 4y2z2 = х4 + 2x3z - 2xz3 - z4 - x/sup>2(x + z)2 + z2(x + z) =; = x4 + 2x3z - 2xz3 - z4 x4 2x3z - x2z2 + z2x2 + 2z3х + z4 = 0.
х4 + 2x3z — 2xz3 - z4 - 4х2у2 + 4y2z2 = х4 + 2x3z - 2xz3 - z4 - x/sup>2(x + z)2 + z2(x + z) =; = x4 + 2x3z - 2xz3 - z4 x4 2x3z - x2z2 + z2x2 + 2z3х + z4 = 0.