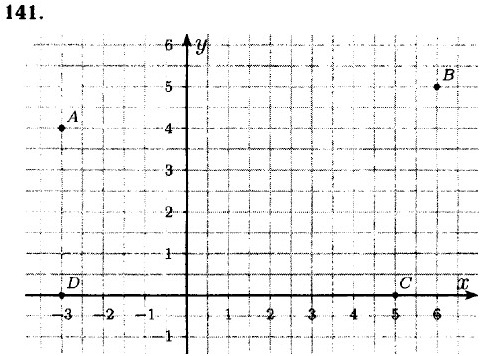
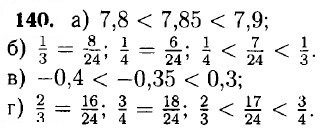|
|
|
|
Главная >> Решенния упражнений к учебнику Макарычева. Алгебра 7 класс |
|
|
Решенния упражнений Линейное уравнение с одной переменной (окончание)134. а) 85 - 27 = 5 ⇒ 8b = 32 ⇒ b = б) 8b - 27 = -11 ⇒ 86 - 16 ⇒ 6 = в) 8b - 27 = 1,8 ⇒ 8b = 28,8 ⇒ b = г) 8b - 27 = -1 ⇒ 8b = 26 ⇒ b = 135. а) 2m - 13 = m + 3 ⇒ m = 16; б) 3 - 5с + 1 = 1 - с ⇒ 4с = 3 ⇒ с = 136. а) 5у + 3 = 36 - у ⇒ 6у = 33 ⇒ у = в) 1,7у + 37 = 9, 3у - 25 - 14 ⇒ 9, 3у - 1,7у = 37 + 25 + 14 ⇒ 7,6у = 76 ⇒ у = 137. а) 2х + 5 = 2 • (х + 1) + 11 ⇒ 2x + 5 = 2x + 2 + 11 ⇒ 2х - 2х = 2 + 11 - 5 ⇒ 0 ≠ 8 - данное уравнение не имеет решений. б) 5 • (2у - 4) = 2 • (5y - 10) ⇒ 10у - 20 = 10у - 20 ⇒ 10у - 10у = 20 - 20 ⇒ 0 = 0 - корнем данного уравнения является любое число. в) 3у - (у - 19) = 2у ⇒ 3у - у + 19 = 2у ⇒ 3у - у - 2у = -19 ⇒ 0 ≠ -19 - данное уравнение не имеет решений. г) 6x = 1 - (4 - 6x) ⇒ 6x = 1 - 4 + 6х =+ 6x - 6х = -3 ⇒ 0 ≠ -3 - данное уравнение не имеет решений. 138. а) 15 • (х + 2) - 30 = 12х ⇒ 15х + 30 - 30 = 12х ⇒ 15х = 12х ⇒ 3х = 0 ⇒ х = 0; б) 6 • (1 + 5х) = 5 • (1 + 6х) ⇒ 6 + 30х = 5 + 30х ⇒ 30х - 30х = 5 - 6 ⇒ 0 ≠ -1 - данное уравнение не имеет решений. в) 3у + (у - 2) = 2 • (2у - 1) ⇒ 3у + у - 2 = 4у - 2 ⇒ 4у - 4у = 2 - 2 ⇒ 0 = 0 - корнем данного уравнения является любое число. г) 6у - (у - 1) = 4 + 5у ⇒ 6у - у + 1 = 4 + 5у ⇒ 5у - 5у = 4 - 1 ⇒ 0 ≠ 3 - данное уравнение не имеет решений. 139. а) -5 < у < 2. у ∈ {-4; -3; -2; -1; 0; 1}; б) 28 ≤ у ≤ 31,2. у ∈ {28; 29; 30; 31}.
142. а) 6,8с - (3,6с + 2,1) = 6,8с - 3,6с - 2,1 = 3,2с - 2,1: при с = 2,5 ⇒ 3,2 • 2,5 - 2,1 = 8 - 2,1 = 5,9. б) 4,4 - (9,6 - 1,2m) = 4,4 - 9,6 + 1, 2m - 1,2m - 5,2: при m = -3,5 ⇒ 1,2 • (-3,5) - 5,2 = -4,2 - 5,2 = -9,4.
|
|
|



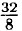 = 4;
= 4;
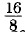 = 2.
= 2.
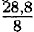 = 3,6.
= 3,6.
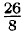 = 3,25.
= 3,25.
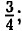 в) 2х + 1 - 20 = 8x + 5 ⇒ 6х = 1 - 20 - 5 ⇒ 6х = -24 ⇒ x =
в) 2х + 1 - 20 = 8x + 5 ⇒ 6х = 1 - 20 - 5 ⇒ 6х = -24 ⇒ x = 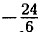 = -4; г) 3ж = 45 - 10x ⇒ 13х = 45 ⇒ х =
= -4; г) 3ж = 45 - 10x ⇒ 13х = 45 ⇒ х = 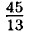 =
= 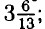 д) 9 - у = 2у ⇒ 3у = 9 ⇒ у = 3.
д) 9 - у = 2у ⇒ 3у = 9 ⇒ у = 3.
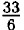 =
= 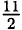 =
= 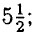
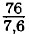 = 10.
= 10.