|
|
|
|
|
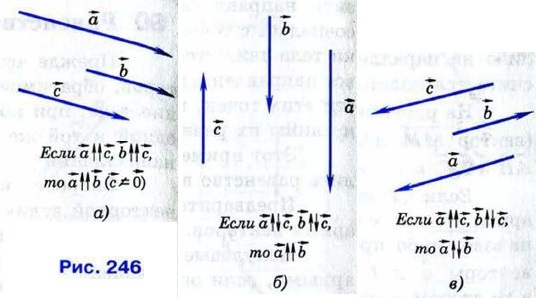
§ 1. Понятие вектора Равенство векторов (окончание)Сонаправленность векторов Начало нулевого вектора совпадает с его концом, поэтому нулевой вектор не имеет какого-либо определённого направления. Иначе говоря, любое направление можно считать направлением нулевого вектора. Условимся считать, что нулевой вектор сонаправлен с любым вектором. Таким образом, на рисунке 245 Ненулевые коллинеарные векторы обладают свойствами, которые проиллюстрированы на рисунке 246, а — в.
Дадим теперь определение равных векторов. Определение
Таким образом, векторы
|
|
|



 и
и  обозначается следующим образом:
обозначается следующим образом: 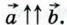 Если же векторы
Если же векторы  На рисунке 245 изображены как сонаправленные, так и противоположно направленные векторы:
На рисунке 245 изображены как сонаправленные, так и противоположно направленные векторы: 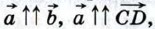
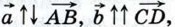
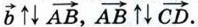
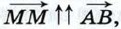
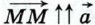 и т. д.
и т. д.
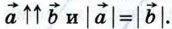 Равенство векторов
Равенство векторов