|
|
§ 2. Сложение и вычитание векторов



Сумма двух векторов (окончание)
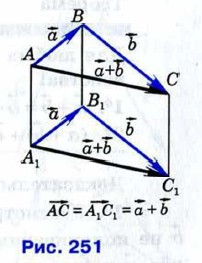
Докажем, что если при сложении векторов  и и  точку А, от которой откладывается вектор точку А, от которой откладывается вектор 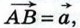 заменить другой точкой А1 то вектор заменить другой точкой А1 то вектор 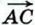 заменится равным ему вектором заменится равным ему вектором 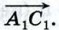 Иными словами, докажем, что если Иными словами, докажем, что если 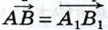 и и 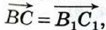 то то 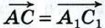 (рис. 251). (рис. 251).
Допустим, что точки А, В, А1, точки В, С, В, и точки А, С, А1 не лежат на одной прямой (остальные случаи рассмотрите самостоятельно). Из равенства 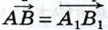 следует, что стороны АВ и А1В1 четырёхугольника АВВ1А1 равны и параллельны, поэтому этот четырёхугольник — параллелограмм. Следовательно, следует, что стороны АВ и А1В1 четырёхугольника АВВ1А1 равны и параллельны, поэтому этот четырёхугольник — параллелограмм. Следовательно, 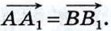 Аналогично из равенства Аналогично из равенства 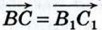 следует, что четырёхугольник ВСС1В1 — параллелограмм. Поэтому следует, что четырёхугольник ВСС1В1 — параллелограмм. Поэтому 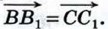 На основе полученных равенств заключаем, что На основе полученных равенств заключаем, что 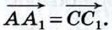 Поэтому AA1C1C — параллелограмм, и, значит, Поэтому AA1C1C — параллелограмм, и, значит, 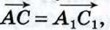 что и требовалось доказать. что и требовалось доказать.
Сумма векторов  и и  обозначается так: обозначается так: 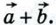
Складывая по правилу треугольника произвольный вектор  с нулевым вектором, получаем, что для любого вектора с нулевым вектором, получаем, что для любого вектора  справедливо равенство справедливо равенство
Правило треугольника можно сформулировать также следующим образом: если А, В и С — произвольные точки, то 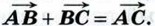 Подчеркнём, что это равенство справедливо для произвольных точек А, В и С, в частности, в том случае, когда две из них или даже все три совпадают. Подчеркнём, что это равенство справедливо для произвольных точек А, В и С, в частности, в том случае, когда две из них или даже все три совпадают.
<<< К началу
|



 и
и  точку А, от которой откладывается вектор
точку А, от которой откладывается вектор 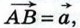 заменить другой точкой А1 то вектор
заменить другой точкой А1 то вектор 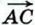 заменится равным ему вектором
заменится равным ему вектором 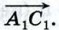 Иными словами, докажем, что если
Иными словами, докажем, что если 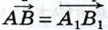 и
и 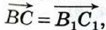 то
то 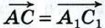 (рис. 251).
(рис. 251).
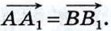 Аналогично из равенства
Аналогично из равенства 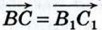 следует, что четырёхугольник ВСС1В1 — параллелограмм. Поэтому
следует, что четырёхугольник ВСС1В1 — параллелограмм. Поэтому 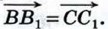 На основе полученных равенств заключаем, что
На основе полученных равенств заключаем, что 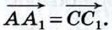 Поэтому AA1C1C — параллелограмм, и, значит,
Поэтому AA1C1C — параллелограмм, и, значит, 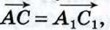 что и требовалось доказать.
что и требовалось доказать.
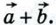
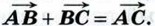 Подчеркнём, что это равенство справедливо для произвольных точек А, В и С, в частности, в том случае, когда две из них или даже все три совпадают.
Подчеркнём, что это равенство справедливо для произвольных точек А, В и С, в частности, в том случае, когда две из них или даже все три совпадают.