|
§ 2. Сложение и вычитание векторов



Законы сложения векторов. Правило параллелограмма
Теорема
Для любых векторов 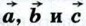 справедливы равенства: справедливы равенства:
10. 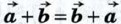 (переместительный закон). (переместительный закон).
20. 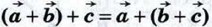 (сочетательный закон). (сочетательный закон).
|
Доказательство
10. Рассмотрим случай, когда векторы  и и  не коллинеарны (случай коллинеарных векторов не коллинеарны (случай коллинеарных векторов  и и  рассмотрите самостоятельно). От произвольной точки А отложим векторы рассмотрите самостоятельно). От произвольной точки А отложим векторы 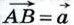 и и 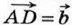 и на этих векторах построим параллелограмм ABCD, как показано на рисунке 252. По правилу треугольника и на этих векторах построим параллелограмм ABCD, как показано на рисунке 252. По правилу треугольника 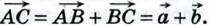 Аналогично Аналогично 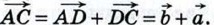 Отсюда следует, что Отсюда следует, что 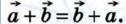
20. От произвольной точки А отложим вектор 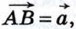 от точки В — вектор от точки В — вектор 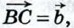 а от точки С — вектор а от точки С — вектор 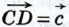 (рис. 253). Применяя правило треугольника, получим: (рис. 253). Применяя правило треугольника, получим:
Отсюда следует, что 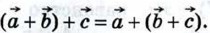 Теорема доказана. Теорема доказана.
При доказательстве утверждения 10 мы обосновали так называемое правило параллелограмма сложения неколлинеарных векторов: чтобы сложить неколлинеарные векторы  и и  , нужно отложить от какой-нибудь точки А векторы , нужно отложить от какой-нибудь точки А векторы 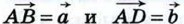 и построить параллелограмм ABCD (см. рис. 252). Тогда вектор и построить параллелограмм ABCD (см. рис. 252). Тогда вектор  равен равен  Правило параллелограмма часто используется в физике, например при сложении двух сил. Правило параллелограмма часто используется в физике, например при сложении двух сил.
| 


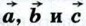 справедливы равенства:
справедливы равенства:
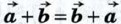 (переместительный закон).
(переместительный закон).
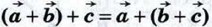 (сочетательный закон).
(сочетательный закон). и
и  не коллинеарны (случай коллинеарных векторов
не коллинеарны (случай коллинеарных векторов 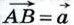 и
и 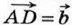 и на этих векторах построим параллелограмм ABCD, как показано на рисунке 252. По правилу треугольника
и на этих векторах построим параллелограмм ABCD, как показано на рисунке 252. По правилу треугольника 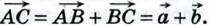 Аналогично
Аналогично 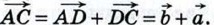 Отсюда следует, что
Отсюда следует, что 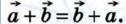
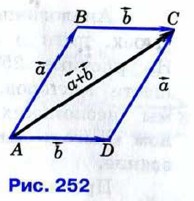
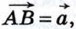 от точки В — вектор
от точки В — вектор 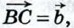 а от точки С — вектор
а от точки С — вектор 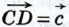 (рис. 253). Применяя правило треугольника, получим:
(рис. 253). Применяя правило треугольника, получим:
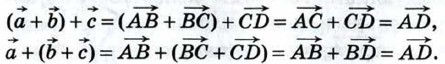
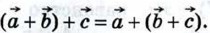 Теорема доказана.
Теорема доказана.
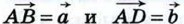 и построить параллелограмм ABCD (см. рис. 252). Тогда вектор
и построить параллелограмм ABCD (см. рис. 252). Тогда вектор 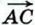 равен
равен  Правило параллелограмма часто используется в физике, например при сложении двух сил.
Правило параллелограмма часто используется в физике, например при сложении двух сил.