|
|
|
|
|
Глава V. Четырёхугольники Ответы к задачам повышенной трудности: глава V. Четырёхугольники811. Указание. Продолжив через одну стороны данного шестиугольника, получить равносторонний треугольник. 812. Указание. Сначала доказать, что а1 + а2 + а3 = а3 + а4 + а5 = а5 + а6 + а1. Затем построить равносторонний треугольник, сторона которого равна а1 + а2 + а3, и воспользоваться задачей 811. 814. Указание. Пусть ABCD — выпуклый четырёхугольник. Учесть, что вершина С лежит внутри угла BAD, поэтому луч АС проходит внутри этого угла и, следовательно, пересекает отрезок BD. Аналогично рассмотреть луч BD и угол АВС. 815. Указание. Если данный четырёхугольник ABCD выпуклый, то воспользоваться задачей 814. Если ABCD — невыпуклый четырёхугольник и, например, прямая АВ пересекает сторону CD в точке М, то рассмотреть два случая: А — точка отрезка МВ и В — точка отрезка AM. 816. Указание. Пусть Р — точка пересечения прямых DE и АВ, DO || АС и О ∈ АВ. Сначала доказать, что АРЕ, AOD и POD — равнобедренные треугольники. 817. Указание. Сначала доказать неравенства 818. Указание. Сначала доказать, что диагонали данного четырёхугольника точкой пересечения делятся пополам. 819. Прямая, параллельная данной прямой. 820. Указание. Воспользоваться задачами 388, а и 389, а. 821. Указание. Воспользоваться задачей 428. 822. Указание. Пусть О1, О2, О3, О4 — точки пересечения диагоналей квадратов, построенных на сторонах АВ, ВС, CD и DA данного параллелограмма ABCD. Сначала доказать равенство треугольников АО1О4, ВО1О2, СО2О3, DО3О4. 823. Указание. На луче АВ отложить отрезок AN, равный отрезку AM, провести отрезок MN и провести высоту NS треугольника AMN. Затем доказать, что 824. 90°. Указание. Пусть D1 — точка, симметричная точке D относительно точки Е. Сначала доказать, что 825. 30°. Указание. На луче AM отложить отрезок АК = АВ и, рассмотрев 826. Указание. Сначала доказать, что 827. Указание. Сначала построить равнобедренный треугольник, основание которого равно сумме оснований трапеции, а боковая сторона равна диагонали трапеции. 828. а) Указание. Сначала доказать, что ось симметрии пересекает одну из сторон треугольника.
|
|
|



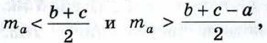 где а, b, с — стороны треугольника, ma — медиана, проведённая к стороне а.
где а, b, с — стороны треугольника, ma — медиана, проведённая к стороне а.
 ANS =
ANS =