|
|
|
|
|
§ 3. Уравнения окружности и прямой Уравнение прямойВыведем уравнение данной прямой l в заданной прямоугольной системе координат. Отметим две точки А (x1; у1) и В (х2; у2) так, чтобы прямая l была серединным перпендикуляром к отрезку АВ (рис. 287, а). Если точка М (х; у) лежит на прямой l, то АМ = ВМ, или AM2 = ВМ2, т. е. координаты точки М удовлетворяют уравнению (x - х1)2 + (у - у1)2 = (х- х2)2 + (у - у2)2. (2)
Если же точка М (x; у) не лежит на прямой l, то AM2 ≠ ВМ2, и, значит, координаты точки М не удовлетворяют уравнению (2). Следовательно, уравнение (2) является уравнением прямой I в заданной системе координат. После возведения выражений в скобках в квадрат и приведения подобных членов уравнение (2) принимает вид ах + bу + с = 0, (3) где а = 2 (х1 - х2), b = 2(у1 - у2), Если в уравнении (3) коэффициент b отличен от нуля, то это уравнение можно записать так: y = kx + d, где
Выведем уравнение прямой l, проходящей через точку М0 (x0; у0) и параллельной оси Оу (рис. 287, б). Абсцисса любой точки М (х; у) прямой l равна x0, т. е. координаты любой точки М (x; у) прямой l удовлетворяют уравнению х = х0. В то же время координаты любой точки, не лежащей на прямой l, этому уравнению не удовлетворяют. Следовательно, уравнение х = х0 является уравнением прямой l. Ясно, что ось Ох имеет уравнение у = О, а ось Оу — уравнение х = 0.
|
|
|




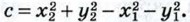 Так как А (x1; у1) и В (x2; y2) — различные точки, то хотя бы одна из разностей (х1 - х2) и (у1 - у2) не равна нулю, т. е. хотя бы один из коэффициентов а и b отличен от нуля. Таким образом, уравнение прямой в прямоугольной системе координат является уравнением первой степени.
Так как А (x1; у1) и В (x2; y2) — различные точки, то хотя бы одна из разностей (х1 - х2) и (у1 - у2) не равна нулю, т. е. хотя бы один из коэффициентов а и b отличен от нуля. Таким образом, уравнение прямой в прямоугольной системе координат является уравнением первой степени.
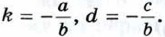 Число k называется угловым коэффициентом прямой, заданной этим уравнением. Докажите самостоятельно, что:
Число k называется угловым коэффициентом прямой, заданной этим уравнением. Докажите самостоятельно, что: