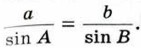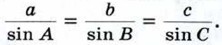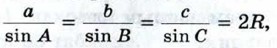|
|
|
|
|
§ 2. Соотношения между сторонами и углами треугольника Теорема синусовТеорема
Доказательство Пусть в треугольнике АВС АВ = с, ВС = а, СА = b. Докажем, что
По теореме о площади треугольника
Из первых двух равенств получаем: Итак, Теорема доказана. Замечание Можно доказать (см. задачу 1033), что отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной окружности. Следовательно, для любого треугольника АВС со сторонами АВ = с, ВС = а и С А = b имеют место равенства
где R — радиус описанной окружности.
|
|
|



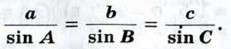
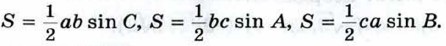
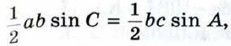 откуда
откуда 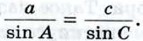 Точно так же из второго и третьего равенств следует,
Точно так же из второго и третьего равенств следует,