|
|
|
|
|
§ 2. Соотношения между сторонами и углами треугольника Теорема косинусовТеорема
Доказательство Пусть в треугольнике АВС АВ = с, ВС = а, СА = b. Докажем, например, что а2 = b2 + с2 - 2bc cos А. (1)
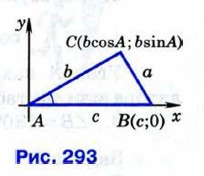
Введём систему координат с началом в точке А так, как показано на рисунке 293. Тогда точка В будет иметь координаты (с; 0), а точка С — координаты (b cos A; b sin А). По формуле расстояния между двумя точками получаем: ВС2 - a2 = (b cos А - с)2 + b2 sin2 А =
Теорема доказана. Теорему косинусов называют иногда обобщённой теоремой Пифагора. Такое название объясняется тем, что в теореме косинусов содержится как частный случай теорема Пифагора. В самом деле, если в треугольнике АВС угол А прямой, то cos А = cos 90° = 0 и по формуле (1) получаем а2 = b2 + с2, т. е. квадрат гипотенузы равен сумме квадратов катетов.
|
|
|