|
|
|
|
|
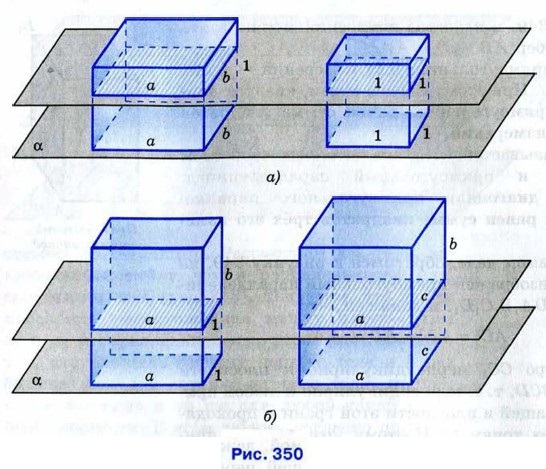
§ 1. Многогранники Свойства прямоугольного параллелепипеда (окончание)Для доказательства этого утверждения воспользуемся принципом Кавальери. Рассмотрим сначала прямоугольный параллелепипед с измерениями a, b, 1 и куб с ребром 1, «стоящие» на плоскости α (рис. 350, а). Этот куб является единицей измерения объёмов, т. е. его объём равен 1. Любая секущая плоскость, параллельная плоскости α, даёт в качестве сечения куба квадрат площади 1, а в качестве сечения рассматриваемого параллелепипеда — прямоугольник площади ab (см. рис. 350, а). Следовательно, согласно принципу Кавальери, объём этого параллелепипеда в ab раз больше объёма куба, т. е. равен аb.
Рассмотрим теперь два прямоугольных параллелепипеда: один с измерениями а, b, 1, а другой — с измерениями а, b, с, «стоящие» на плоскости α так, как показано на рисунке 350, б. Объём первого параллелепипеда, как было доказано, равен ab. Докажем, что объём второго параллелепипеда равен abc. Любая секущая плоскость, параллельная плоскости α, даёт в качестве сечения первого параллелепипеда прямоугольник площади α, а в качестве сечения второго — прямоугольник площади ас (см. рис. 350, б). Поэтому объём V второго параллелепипеда в с раз больше объёма первого и, следовательно, равен V = abc, что и требовалось доказать. В прямоугольном параллелепипеде с измерениями а, b, с, изображённом на рисунке 350, б, площадь S основания равна ас, а высота h равна боковому ребру: h = b. Поэтому формулу V = abc можно записать в виде V = Sh, т. е. объём прямоугольного параллелепипеда равен произведению площади основания на высоту. Оказывается, что в точности такая же формула имеет место для любой призмы: объём призмы равен произведению площади основания на высоту. Это утверждение нетрудно доказать с помощью принципа Кавальери (см. задачу 1198).
|
|
|