|
§ 1. Многогранники



Пирамида (окончание)
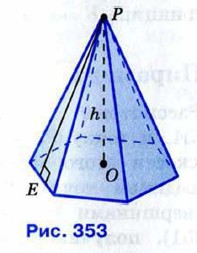
На рисунке 353 отрезок РЕ — одна из апофем. Можно доказать, что все апофемы правильной пирамиды равны друг другу (задача 1205).
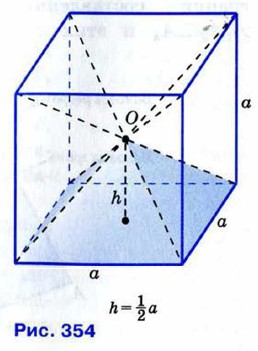
Рассмотрим куб со стороной а и проведём его диагонали (рис. 354). В результате куб окажется разбитым на шесть равных друг другу правильных четырёхугольных пирамид с общей вершиной в точке пересечения диагоналей куба. У каждой из этих пирамид основанием является квадрат со стороной а, высота равна 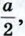 а объём в шесть раз меньше объёма куба, т. е. равен а объём в шесть раз меньше объёма куба, т. е. равен 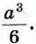
Но 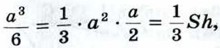 где S = а2 — площадь основания пирамиды, где S = а2 — площадь основания пирамиды, 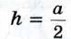 — её высота. Таким образом, объём правильной четырёхугольной пирамиды со стороной основания а и высотой h равен одной трети произведения площади основания на высоту. Основываясь на этом факте, можно доказать (см. задачу 1210), что аналогичное утверждение справедливо и для произвольной пирамиды: объём пирамиды равен одной трети произведения площади основания на высоту. — её высота. Таким образом, объём правильной четырёхугольной пирамиды со стороной основания а и высотой h равен одной трети произведения площади основания на высоту. Основываясь на этом факте, можно доказать (см. задачу 1210), что аналогичное утверждение справедливо и для произвольной пирамиды: объём пирамиды равен одной трети произведения площади основания на высоту.
<<< К началу
| 


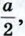 а объём в шесть раз меньше объёма куба, т. е. равен
а объём в шесть раз меньше объёма куба, т. е. равен 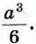
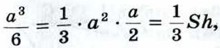 где S = а2 — площадь основания пирамиды,
где S = а2 — площадь основания пирамиды, 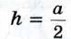 — её высота. Таким образом, объём правильной четырёхугольной пирамиды со стороной основания а и высотой h равен одной трети произведения площади основания на высоту. Основываясь на этом факте, можно доказать (см. задачу 1210), что аналогичное утверждение справедливо и для произвольной пирамиды: объём пирамиды равен одной трети произведения площади основания на высоту.
— её высота. Таким образом, объём правильной четырёхугольной пирамиды со стороной основания а и высотой h равен одной трети произведения площади основания на высоту. Основываясь на этом факте, можно доказать (см. задачу 1210), что аналогичное утверждение справедливо и для произвольной пирамиды: объём пирамиды равен одной трети произведения площади основания на высоту.