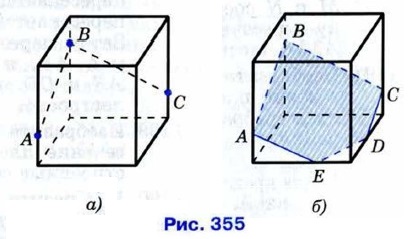
Задачи к § 1. Многогранники

1184. Сколько граней, рёбер и вершин имеет: а) прямоугольный параллелепипед; б) тетраэдр; в) октаэдр?

1185. Докажите, что число вершин любой призмы чётно, а число рёбер кратно 3.

1186. Докажите, что площадь боковой поверхности прямой призмы (т. е. сумма площадей её боковых граней) равна произведению периметра основания на боковое ребро.

1187. Существует ли параллелепипед, у которого: а) только одна грань — прямоугольник; б) только две смежные грани — ромбы; в) все углы граней острые; г) все углы граней прямые; д) число всех острых углов граней не равно числу всех тупых углов граней?

1188. На трёх рёбрах параллелепипеда даны точки А, В и С. Постройте сечение параллелепипеда плоскостью, проходящей через эти точки.

Решение

При построении сечений параллелепипеда нужно руководствоваться следующим правилом (оно будет обосновано в курсе стереометрии в 10 классе): отрезки, по которым секущая плоскость пересекает две противоположные грани параллелепипеда, параллельны.

1) Рассмотрим сначала случай расположения точек А, В и С, изображённый на рисунке 355, а. Проведём отрезки АВ и ВС. Далее, руководствуясь указанным правилом, через точку А проведём в плоскости «передней» грани прямую, параллельную ВС, а через точку С в плоскости боковой грани проведём прямую, параллельную АВ. Пересечения этих прямых с рёбрами нижней грани дают точки Е и D (рис. 355, б). Остаётся провести отрезок DE, и искомое сечение — пятиугольник ABCDE — построено.

Рис. 355

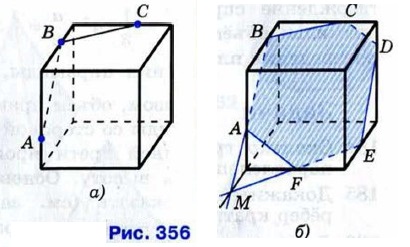
2) Обратимся теперь к случаю, представленному на рисунке 356,а. Этот случай более трудный, чем предыдущий. Можно провести отрезки АВ и ВС (см. рис. 356, а), но что делать дальше? Поступим так. Сначала построим прямую, по которой секущая плоскость пересекается с плоскостью нижнего основания параллелепипеда. С этой целью продолжим отрезок АВ и нижнее ребро, лежащее в той же грани, что и отрезок АВ, до пересечения в точке М (рис. 356, б). Далее, через точку М проведём в плоскости нижнего основания прямую, параллельную ВС. Это и есть та прямая, по которой секущая плоскость пересекается с плоскостью нижнего основания. Эта прямая пересекается с рёбрами нижнего основания в точках Е и F. Затем через точку Е проведём прямую, параллельную прямой АВ, и получим точку D. Наконец, проведём отрезки AF и CD, и искомое сечение — шестиугольник ABCDEF — построено.

Рис. 356

1189. Изобразите параллелепипед ABCDA₁B₁C₁D₁ и постройте его сечение плоскостью¹: а) АВС₁: б) АСС₁. Докажите, что построенные сечения — параллелограммы.

¹ Для краткости записи плоскость, проходящую через точки А, В и С₁, мы называем плоскостью АВС₁; аналогичные обозначения плоскостей используются и в других задачах.

1190. Изобразите параллелепипед ABCDA₁B₁C₁D₁ и отметьте точки М и N соответственно на рёбрах ВВ₁ и СС₁. Постройте точку пересечения: а) прямой MN с плоскостью АВС; б) прямой AM с плоскостью А₁В₁С₁.

1191. Изобразите параллелепипед ABCDA₁B₁C₁D₁ и постройте его сечение плоскостью, проходящей через точки В₁, D₁ и середину ребра CD. Докажите, что построенное сечение — трапеция.

1192. Изобразите параллелепипед ABCDA₁B₁C₁D₁ и постройте его сечение плоскостью MNK, где точки М, N и К лежат соответственно на рёбрах: а) ВВ₁, АА₁, AD; б) СС₁, AD, ВВ₁.

1193. Найдите диагональ прямоугольного параллелепипеда, если его измерения равны а) 1, 1, 2; б) 8, 9, 12; в) √39, 7, 9.

1194. Ребро куба равно а. Найдите диагональ этого куба.

1195. Тело R состоит из тел Р и Q, имеющих соответственно объёмы V₁ и V₂. Выразите объём V тела R через V₁ и V₂, если:

а) тела Р и Q не имеют общих внутренних точек;
б) тела Р и Q имеют общую часть, объём которой равен

Продолжение >>>