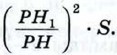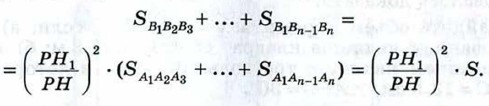|
|
|
|
|
§ 1. Многогранники Задачи к § 1. Многогранники (продолжение)1196. Измерения прямоугольного параллелепипеда равны 8 см, 12 см и 18 см. Найдите ребро куба, объём которого равен объёму этого параллелепипеда. 1197. Найдите объём прямоугольного параллелепипеда ABCDA1B1C1D1, если АС1 = 13 см, BD= 12 см и ВС1 = 11 см. 1198. Докажите, что объём призмы равен произведению площади основания на высоту. Решение Воспользуемся принципом Кавальери. Рассмотрим призму и прямоугольный параллелепипед с площадями оснований, равными S, и высотами, равными h, «стоящие» на одной плоскости (рис. 357).
Докажем, что объём призмы равен Sh. Любая секущая плоскость, параллельная плоскости оснований, даёт в качестве сечения призмы равный её основанию многоугольник площади S, а в качестве сечения прямоугольного параллелепипеда — прямоугольник площади S. Следовательно, объём призмы равен объёму параллелепипеда. Но объём прямоугольного параллелепипеда равен произведению площади основания на высоту, т. е. равен Sh. Поэтому и объём призмы равен Sh. 1199. Найдите объём прямой призмы АВСА1В1С1, если ∠BAC= 120°, АВ = 5 см, АС = 3 см, а наибольшая из площадей боковых граней равна 35 см2. 1200. Найдите объём правильной «-угольной призмы, все рёбра ко торой равны а, если: а) n = 3; б) n = 4; в) n = 6; г) n = 8. 1201. Существует ли тетраэдр, у которого пять углов граней — прямые? 1202. Изобразите тетраэдр DABC и на рёбрах DB, DC и ВС отметьте соответственно точки М, N и К. Постройте точку пересечения: а) прямой MN и плоскости АВС; б) прямой KN и плоскости ABD. 1203. Изобразите тетраэдр KLMN и постройте сечение этого тетраэдра плоскостью, проходящей через ребро KL и середину А ребра MN. 1204. Изобразите тетраэдр DABC, отметьте точки М и N на рёбрах BD и CD и внутреннюю точку К грани АВС. Постройте сечение тетраэдра плоскостью MNK. 1205. Докажите, что все апофемы правильной пирамиды равны друг другу. 1206. Докажите, что площадь боковой поверхности правильной пирамиды (т. е. сумма площадей её боковых граней) равна половине произведения периметра основания на апофему. 1207. Основанием пирамиды является ромб, сторона которого равна 5 см, а одна из диагоналей равна 8 см. Найдите боковые рёбра пирамиды, если её высота проходит через точку пересечения диагоналей основания и равна 7 см. 1208. Найдите площадь боковой поверхности правильной шестиугольной пирамиды, если сторона её основания равна а, а площадь боковой грани равна площади сечения, проведённого через вершину пирамиды и большую диагональ основания. 1209.* Через точку Н1 высоты PH пирамиды РА1А2...Аn проведена секущая плоскость β, параллельная плоскости α её основания. Докажите, что площадь полученного сечения равна Решение Докажем это утверждение сначала для треугольной пирамиды, а затем — для произвольной пирамиды. Рассмотрим треугольную пирамиду РА1А2А3 и докажем, что рассматриваемое сечение представляет собой треугольник В1В2В3, подобный треугольнику А1А2А3 с коэффициентом подобия
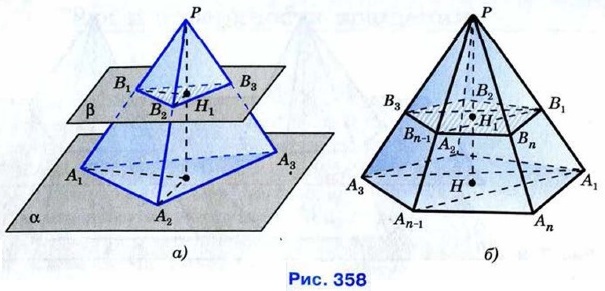
Рассмотрим теперь произвольную пирамиду. Её можно разбить на треугольные пирамиды с общей высотой РН (на рисунке 358, б показано разбиение выпуклой пятиугольной пирамиды). Поэтому площадь сечения равна
|
|
|



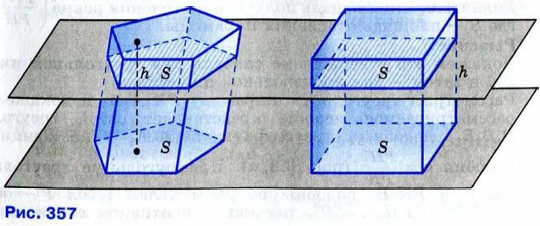
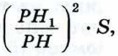 где S — площадь основания пирамиды.
где S — площадь основания пирамиды.
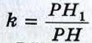 (рис. 358, а). Прямоугольные треугольники РНА1 и РН1В1 подобны по двум углам (угол Р — общий; ∠PH1B1 = ∠PHA1 = 90°, так как в противном случае прямые НА1 и Н1В1, а значит, и плоскости α и β пересекались бы, что противоречит условию), поэтому
(рис. 358, а). Прямоугольные треугольники РНА1 и РН1В1 подобны по двум углам (угол Р — общий; ∠PH1B1 = ∠PHA1 = 90°, так как в противном случае прямые НА1 и Н1В1, а значит, и плоскости α и β пересекались бы, что противоречит условию), поэтому 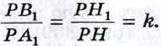 Аналогично из подобия треугольников РНА2 и РН1В2 находим:
Аналогично из подобия треугольников РНА2 и РН1В2 находим: 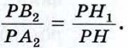 Таким образом,
Таким образом, 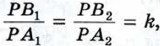 откуда следует, что треугольники РВ1В2 и РА1А2 подобны по второму признаку подобия треугольников. Поэтому
откуда следует, что треугольники РВ1В2 и РА1А2 подобны по второму признаку подобия треугольников. Поэтому 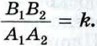 Точно так же доказывается, что
Точно так же доказывается, что 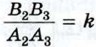 и
и 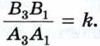 Таким образом, треугольники В1В2В3 и А1А2А3 подобны с коэффициентом подобия
Таким образом, треугольники В1В2В3 и А1А2А3 подобны с коэффициентом подобия 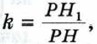 и, следовательно, площадь треугольника В1В2В3 равна
и, следовательно, площадь треугольника В1В2В3 равна