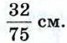|
|
|
|
|
Глава XIV. Начальные сведения из стереометрии Дополнительные задачи к главе XIV. Начальные сведения из стереометрии (окончание)1250. Вычислите площадь основания и высоту конуса, если развёрткой его боковой поверхности является сектор, радиус которого равен 9 см, а дуга равна 120°. 1251. Равнобедренный треугольник, боковая сторона которого равна m, а угол при основании равен φ, вращается вокруг основания. Найдите площадь поверхности тела, полученного при этом вращении. 1252. Шар и цилиндр имеют равные объёмы, а диаметр шара равен диаметру цилиндра. Выразите высоту цилиндра через радиус шара. 1253. В цилиндрическую мензурку диаметром 2,5 см, наполненную водой до некоторого уровня, опускают 4 равных металлических шарика диаметром 1 см. На сколько изменится уровень воды в мензурке? 1254. Вода покрывает приблизительно 1255. В каком отношении находятся объёмы двух шаров, если площади их поверхностей относятся как m2 : n2? Ответы к дополнительные задачам: Глава XIV. Начальные сведения из стереометрии1232. Указание. Воспользоваться неравенством треугольника. 1233. Указание. Воспользоваться тем, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон. 1234. б) Указание. Сначала построить отрезок, по которому секущая плоскость пересекает грань AA1D1D. 1235. Параллелограмм BKD1L. 1236. 2√122 дм. 1237. а) 432√2 см3; б) 6√6; в) 0,32√5 см3. 1238. 1239. 72 см3. 1241. (2√34 + 22) м2. 1242. 1692 см3. 1243. 1244. ≈ 208 м. 1245. ≈ 61 кг. 1246. 6√2 см, 18 см. 1247. 1248. 375 см3. 1249. 216°. 1250. 9π см2, 6 см. 1251. 2πm2 sin φ. 1252. 1253. Уровень воды повысится на 1254. 63752π км2 ≈ 1,28 • 108 км2. 1255. m3 : n3.
|
|
|



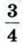 земной поверхности. Сколько квадратных километров земной поверхности занимает суша (радиус Земли считать равным 6375 км)?
земной поверхности. Сколько квадратных километров земной поверхности занимает суша (радиус Земли считать равным 6375 км)?
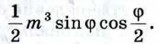
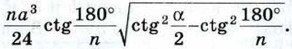
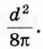
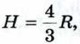 где Н — высота цилиндра, R — радиус шара.
где Н — высота цилиндра, R — радиус шара.