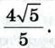|
|
|
|
|
Глава X. Метод координат Ответы на задачи повышенной трудности к главе X. Метод координат1256. Указание. Использовать координаты середин диагоналей АС и BD. 1257. Указание. Воспользоваться тем, что отношение соответствующих координат векторов 1258. 1259. 1260. 3√5 см. Указание. Принять за оси координат прямые AM и BN. 1261. 1262. 1263. Указание, а) Пусть L — линия, заданная данным уравнением, а М0 (x0; у0) — некоторая её точка. Написать уравнение серединного перпендикуляра к отрезку М1М2, где М1 (х0 - А; у0 - В), М2(х0 + А; у0 + В), и убедиться в том, что оно совпадает с данным уравнением, б) Учесть, что уравнение любой окружности не содержит членов вида kxy, где k — число, k ≠ 0. 1264. (1; 0), (-0,6; 0,8), 1265. а) Окружность, точка или пустое множество. б) Прямая, вся плоскость или пустое множество. Указание. Вывести уравнение искомого множества точек. 1266. Окружность без одной точки. Указание. Вывести уравнение искомого множества точек, задав систему координат так, чтобы прямая а совпала с одной из осей координат, а точка А лежала на другой оси. 1267. Окружность радиуса kR, где R — радиус данной окружности. Указание. Ввести систему координат с началом О и вывести уравнение искомого множества. 1268. б) Указание. Воспользоваться теоремой, обратной теореме Пифагора.
|
|
|



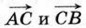 равно λ.
равно λ.
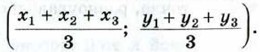 Указание. Воспользоваться задачей 1257.
Указание. Воспользоваться задачей 1257.
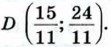 Указание. Воспользоваться задачами 535 и 1257.
Указание. Воспользоваться задачами 535 и 1257.
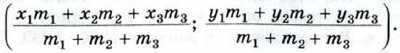
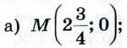 б) М(2; 0). Указание. Воспользоваться тем, что если две точки лежат по разные стороны от оси абсцисс, то искомая точка является точкой пересечения отрезка с концами в этих точках и оси абсцисс.
б) М(2; 0). Указание. Воспользоваться тем, что если две точки лежат по разные стороны от оси абсцисс, то искомая точка является точкой пересечения отрезка с концами в этих точках и оси абсцисс.