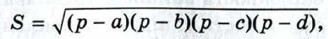|
|
|
|
|
Глава XI. Соотношения между сторонами и углами треугольника. Скалярное произведение векторов Задачи повышенной трудности к главе XI. Соотношения между сторонами и углами треугольника. Скалярное произведение векторов1269. На сторонах квадрата MNPQ взяты точки А и В так, что
1270. Диагонали АС и BD четырёхугольника ABCD пересекаются в точке О. Площадь треугольника ODC есть среднее пропорциональное между площадями треугольников ОВС и OAD. Докажите, что ABCD — трапеция с основаниями AD и ВС или параллелограмм. 1271. Докажите, что площадь S произвольного четырёхугольника со сторонами a, b, с, d (последовательно) удовлетворяет неравенству 1272. Докажите, что в треугольнике АВС биссектриса АА1 вычисляется по формуле 1273. Выразите диагонали вписанного в окружность четырёхугольника через его стороны. 1274. Докажите, что площадь четырёхугольника, вписанного в окружность, может быть вычислена по формуле
где р — полупериметр, a, b, с, d — стороны четырёхугольника. 1275. Докажите, что стороны треугольника образуют арифметическую прогрессию тогда и только тогда, когда прямая, проходящая через центры вписанной и описанной окружностей, перпендикулярна к одной из биссектрис треугольника. 1276. В прямоугольной трапеции ABCD меньшее основание AD равно 3, а боковая сторона CD, не перпендикулярная к основаниям, равна 6. Точка Е — середина отрезка CD, угол С BE равен α. Найдите площадь трапеции ABCD. 1277. В остроугольном треугольнике АВС сторона АВ больше стороны ВС, отрезки AM и CN — высоты треугольника, точка О — центр описанной окружности. Угол АВС равен β, а площадь четырёхугольника NOMB равна S. Найдите сторону АС. 1278. В треугольнике АВС проведены высота АН длиной h, медиана AM длиной l, биссектриса AN. Точка N — середина отрезка МН. Найдите расстояние от вершины А до точки пересечения высот треугольника АВС.
|
|
|



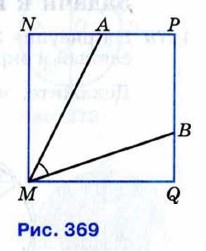
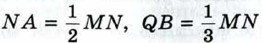 (рис. 369). Докажите, что ∠AMB = 45°.
(рис. 369). Докажите, что ∠AMB = 45°.
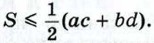
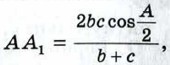 Где b = АС, с = АВ.
Где b = АС, с = АВ.