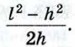|
|
|
|
|
Глава XI. Соотношения между сторонами и углами треугольника. Скалярное произведение векторов Ответы на задачи повышенной трудности к главе XI. Соотношения между сторонами и углами треугольника. Скалярное произведение векторов1269. Указание. Положив MN = a, сначала найти площадь треугольника АМВ и стороны AM и ВМ. 1270. Указание. Доказать, что в любом выпуклом четырёхугольнике ABCD имеет место равенство SODC • SOAB = SOBC • SOAD (О — точка пересечения диагоналей). 1271. Указание. Доказать утверждение сначала для выпуклого четырёхугольника. Для этого провести диагональ, соединяющую общий конец сторон а и d с общим концом сторон b и с, и найти площади получившихся треугольников. 1272. Указание. Воспользоваться тем, что SАВС = SAA1B + SAA1C. 1273. 1274. Указание. Пользуясь теоремой косинусов, доказать, что синус угла, заключённого между сторонами а и b, равен 1275. Указание. Доказать сначала, что прямая, проходящая через центры вписанной и описанной окружностей, перпендикулярна к одной из биссектрис тогда и только тогда, когда вписанная окружность касается одной из сторон треугольника в точке, равноудалённой от середины этой стороны и основания высоты, проведённой к этой стороне. 1276. 72 sin α cos3 α. 1277. 2√Stgβ. 1278.
|
|
|



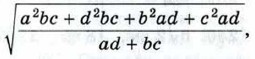
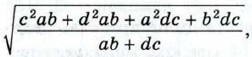 где a, b, c, d — стороны вписанного четырёхугольника.
где a, b, c, d — стороны вписанного четырёхугольника.
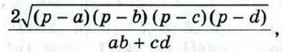 где р — полупериметр.
где р — полупериметр.