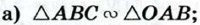|
|
|
|
|
Глава XII. Длина окружности и площадь круга Задачи повышенной трудности к главе XII. Длина окружности и площадь круга1279. На рисунке 370 изображён правильный десятиугольник, вписанный в окружность радиуса R, АС — биссектриса угла ОАВ. Докажите, что:
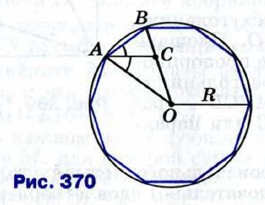
1280. Докажите, что отрезок АК, изображённый на рисунке 371, равен стороне правильного десятиугольника, вписанного в окружность с центром О.
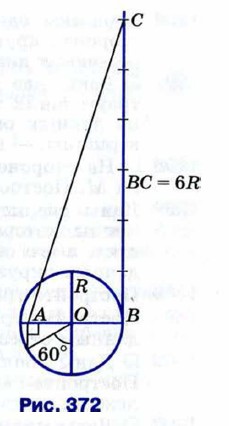
1281. Около правильного пятиугольника А1А2А3А4А5 описана окружность с центром О. Вершинами треугольника АВС являются середины сторон А1А2, А2А3 и А3А4 пятиугольника. Докажите, что центр О данной окружности и центр О1 окружности, вписанной в треугольник АВС, симметричны относительно прямой АС. 1282.* В данную окружность впишите правильный десятиугольник. 1283. В данную окружность впишите правильный пятиугольник. 1284. В данную окружность впишите пятиконечную звезду. 1285. Пусть М — произвольная точка, лежащая внутри правильного n-угольника. Докажите, что сумма перпендикуляров, проведённых из точки М к прямым, содержащим стороны n-угольника, равна nr, где r — радиус вписанной окружности. 1286. Углы треугольника образуют геометрическую прогрессию со знаменателем 2. Докажите, что середины сторон и основания высот этого треугольника являются шестью вершинами правильного семиугольника. 1287. Пусть ABCD — квадрат, a А1В1С1 — правильный треугольник, вписанные в окружность радиуса R. Докажите, что сумма АВ + А1В1 равна длине полуокружности с точностью до 0,01R. 1288. По данным рисунка 372 докажите, что длина отрезка АС равна длине окружности с центром О радиуса R с точностью до 0,001R.
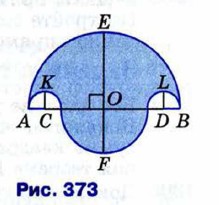
1289. На рисунке 373 изображены четыре полуокружности: АЕВ, АКС, CFD, DLB, причём AC = DB. Докажите, что площадь закрашенной фигуры равна площади круга, построенного на отрезке EF как на диаметре.
Постройте границу круга, площадь которого равна: а) площади кольца между двумя данными концентрическими окружностями;
|
|
|