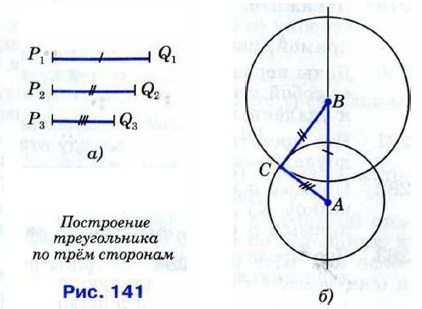
Построение треугольника по трём элементам (окончание)

Задача 2

Построить треугольник по стороне и двум прилежащим к ней углам.

Решите эту задачу самостоятельно.

Задача 3

Построить треугольник по трём его сторонам.

Решение

Пусть даны отрезки P₁Q₁, P₂Q₂ и P₃Q₃ (рис. 141, а). Требуется построить треугольник АВС, в котором AB = P₁Q₁, BC = P₂Q₂, СА = P₃Q₃.

Проведём прямую и на ней с помощью циркуля отложим отрезок АВ, равный отрезку P₁Q₁ (рис. 141,6). Затем построим две окружности: одну — с центром А и радиусом P₃Q₃, а другую — с центром В и радиусом P₂Q₂. Пусть точка С — одна из точек пересечения этих окружностей. Проведя отрезки АС и ВС, получим искомый треугольник АВС.

рис. 141

В самом деле, по построению AB = P₁Q₁, BC = P₂Q₂, CA = P₃Q₃, т. е. стороны треугольника АВС равны данным отрезкам.

Задача 3 не всегда имеет решение. Действительно, во всяком треугольнике сумма любых двух сторон больше третьей стороны, поэтому если какой-нибудь из данных отрезков больше или равен сумме двух других, то нельзя построить треугольник, стороны которого равнялись бы данным отрезкам.

<<< К началу