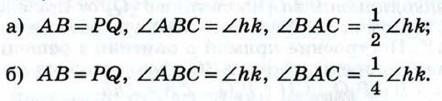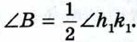|
|
|
|
|
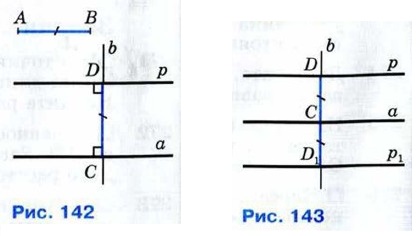
§ 2. Соотношения между сторонами и углами треугольника Задачи к § 4. Построение треугольника по трём элементам271. 272. 273. 274. Докажите, что в равнобедренном треугольнике середина основания равноудалена от боковых сторон. 275. На основании АВ равнобедренного треугольника АВС взята точка М, равноудалённая от боковых сторон. Докажите, что СМ — высота треугольника АВС. 276. 277. Расстояние между параллельными прямыми а и б равно 3 см, а между параллельными прямыми а и с равно 5 см. Найдите расстояние между прямыми b и с. 278. 279.* Докажите, что все точки плоскости, расположенные по одну сторону от данной прямой и равноудалённые от неё, лежат на прямой, параллельной данной. 280. Даны неразвёрнутый угол АВС и отрезок PQ. Что представляет собой множество всех точек, лежащих внутри данного угла и удалённых от прямой ВС на расстояние PQ? 281. Что представляет собой множество всех точек плоскости, равноудалённых от двух данных параллельных прямых? 282. Прямые а и б параллельны. Докажите, что середины всех отрезков ХY, где X ∈ a, Y ∈ б, лежат на прямой, параллельной прямым а и б и равноудалённой от этих прямых. 283. Что представляет собой множество всех точек плоскости, находящихся на данном расстоянии от данной прямой? Задачи на построение284. Решение Отметим на прямой а какую-нибудь точку С и проведём через точку С прямую б, перпендикулярную к прямой а (рис. 142). Затем на одном из лучей прямой б, исходящих из точки С, отложим отрезок CD, равный отрезку АВ. Через точку D проведём прямую р, перпендикулярную к прямой б. Прямая р — искомая (объясните почему). Как видно из построения, для любой данной прямой а и любого данного отрезка АВ искомую прямую можно построить, причём задача имеет два решения (прямые р и р, на рисунке 143).
285. 286. Постройте треугольник по стороне, прилежащему к ней углу и биссектрисе треугольника, проведённой из вершины этого угла. 287. 288. Даны отрезок PQ и угол hk. Постройте треугольник АВС так, чтобы:
289. Даны два угла hk и h1k1 и отрезок PQ. Постройте треугольник АВС так, чтобы AB = PQ, ∠A = ∠hk, 290. 291.
|
|
|



 Из точки к прямой проведены перпендикуляр и наклонная, сумма длин которых равна 17 см, а разность длин равна 1 см. Найдите расстояние от точки до прямой.
Из точки к прямой проведены перпендикуляр и наклонная, сумма длин которых равна 17 см, а разность длин равна 1 см. Найдите расстояние от точки до прямой.