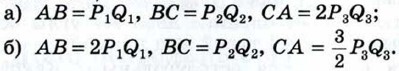|
|
|
|
|
§ 2. Соотношения между сторонами и углами треугольника Задачи к § 4. Построение треугольника по трём элементам (окончание)292.
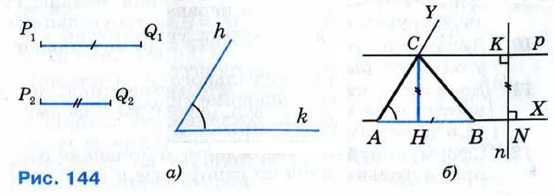
Всегда ли задача имеет решение? 293. Решение Даны отрезки P1Q1 и P2Q2 и угол hk (рис. 144, а). Требуется построить треугольник АВС, у которого одна из сторон, скажем АВ, равна отрезку P1Q1, один из прилежащих к ней углов, например угол А, равен данному углу hk, а высота СН, проведённая к стороне АВ, равна данному отрезку P2Q2. Построим угол XAY, равный данному углу hk, и отложим на луче АХ отрезок АВ, равный данному отрезку P1Q1 (рис. 144, б).
Для построения вершины С искомого треугольника заметим, что расстояние от точки С до прямой АВ должно равняться P2Q2. Множеством всех точек плоскости, находящихся на расстоянии P2Q2 от прямой АВ и лежащих по ту же сторону от прямой АВ, что и точка Y, является прямая р, параллельная прямой АВ и находящаяся на расстоянии Р2Q2 от прямой АВ. Следовательно, искомая точка С есть точка пересечения прямой р и луча AY. Построение прямой р описано в решении задачи 284. Очевидно, треугольник АВС удовлетворяет всем условиям задачи: AB = P1Q1, СН = P2Q2, ∠A = ∠hk. 294. 295. Постройте треугольник по двум сторонам и медиане, проведённой к одной из этих сторон. Ответы к задачам § 4. Построение треугольника по трём элементам271. 8см. 272. 12см. 273. 14см. 275. Указание. Сначала доказать, что СМ — медиана треугольника АВС. 277. 2 см или 8 см. 278. 3 см. 279. Указание. Через одну из точек, удовлетворяющих условию задачи, провести прямую, параллельную данной, и доказать, что любая другая точка, удовлетворяющая условию задачи, лежит на этой прямой. 280. Луч с началом на стороне ВА, параллельный стороне ВС. Указание. Воспользоваться задачей. 279. 281. Прямая, параллельная данным прямым и находящаяся на равных расстояниях от них. 282. Указание. Воспользоваться задачей 281. 283. Две прямые, параллельные данной прямой и расположенные на данном расстоянии по разные стороны от неё. 285. Указание. Воспользоваться задачей 284.
|
|
|



 Даны отрезки P1Q1, P2Q2 и Р3Q3. Постройте треугольник АВС так, чтобы:
Даны отрезки P1Q1, P2Q2 и Р3Q3. Постройте треугольник АВС так, чтобы: