|
|
|
|
|
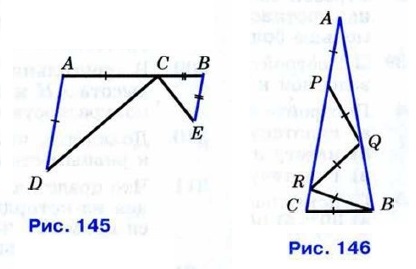
Глава IV. Соотношения между сторонами и углами треугольника Дополнительные задачи к главе IV296. 297. На стороне AD треугольника ADC отмечена точка В так, что BC = BD. Докажите, что прямая DC параллельна биссектрисе угла АВС. 298. На рисунке 145 AD || BE, АС = AD и ВС = ВЕ. Докажите, что угол DCE — прямой.
299. На рисунке 146 АВ = АС, АР = PQ = QR = RB = BC. Найдите угол А. 300. Докажите, что в тупоугольном треугольнике основание высоты, проведённой из вершины тупого угла, лежит на стороне треугольника, а основания высот, проведённых из вершин острых углов, — на продолжениях сторон. 301. Из точки А к прямой а проведены перпендикуляр АН и наклонные АМ1 и АМ2. Докажите, что: а) если НМ1 = НМ2, то АМ1 = АМ2;
302. Из точки А к прямой а проведены перпендикуляр АН и наклонные АМ1 и АМ2. Докажите, что: а) если АМ1 = АМ2, то НМ1 = НМ2,
303*. Докажите, что в треугольнике АВС медиана AM меньше полусуммы сторон АВ и АС. 304*. Докажите, что если точка М лежит внутри треугольника АВС, то МВ + МС < АВ + АС. 305. Докажите, что сумма расстояний от любой точки, лежащей внутри треугольника, до его вершин меньше периметра треугольника. 306. Докажите, что если АВ = АС + СВ, то точки А, В и С лежат на одной прямой. 307. В прямоугольном треугольнике проведена высота из вершины прямого угла. Докажите, что данный треугольник и два образовавшихся треугольника имеют соответственно равные углы. 308. В равнобедренном треугольнике АВС с основанием АС, равным 37 см, внешний угол при вершине В равен 60°. Найдите расстояние от вершины С до прямой АВ. 309. В треугольнике с неравными сторонами АВ и АС проведены высота АН и биссектриса AD. Докажите, что угол HAD равен полуразности углов В и С. 310. Докажите, что в равных треугольниках высоты, проведённые к равным сторонам, равны. 311. Что представляет собой множество всех точек плоскости, каждая из которых равноудалена от двух данных пересекающихся прямых? 312. Отрезок соединяет вершину треугольника с точкой, лежащей на противоположной стороне. Докажите, что этот отрезок меньше большей из двух других сторон. 313*. 314. Постройте прямоугольный треугольник по: а) гипотенузе и острому углу;
|
|
|



 В равнобедренном треугольнике АВС биссектрисы равных углов В и С пересекаются в точке О. Докажите, что угол ВОС равен внешнему углу треугольника при вершине В.
В равнобедренном треугольнике АВС биссектрисы равных углов В и С пересекаются в точке О. Докажите, что угол ВОС равен внешнему углу треугольника при вершине В.